Ромб - це геометрична фігура, у якої всі сторони рівні, тому її периметр, як і периметр квадрата дорівнює стороні, помноженої на 4. Площа ромба залежить не тільки від його боку, але і висоти, так як ромб є паралелограма, ця формула запозичена від нього. Щоб обчислити площу ромба необхідно помножити висоту на його сторону. P = 4a S = ah
Кути ромба також пов'язані з висотою, так як вона утворює всередині ромба прямокутний трикутник. Синус кута α в ромбі дорівнює відношенню висоти, як катета, до сторони ромба, як гіпотенузи. Кут β можна знайти через різницю 180 градусів і кута α. (Ріс.115.1) sinα = h / a β = 180 ° -α
Знаючи будь-який кут ромба, можна знайти його діагоналі. Оскільки діагоналі ромба перетинаються під прямим кутом, вони ділять ромб на чотири конгруентних прямокутних трикутника, катетами яких є половини діагоналей і гіпотенузою - сторона ромба. Відповідно в кожному такому трикутнику, кути рівні половин кутів ромба. Обчислити діагоналі через кут α можна, прирівнявши їх до сторони ромба помноженої на синус або косинус α відповідно. (Ріс.115.2) d_1 = a sin 〖α / 2〗 d_1 = a cos 〖α / 2〗
Так як ромб є рівностороннім многоугольником, отже, в нього можна вписати коло. Радіус вписаного кола з'єднує її центр в точці перетину діагоналей і сторону ромба перпендикулярним їй відрізком. Оскільки єдиним перпендикуляром в ромбі є висота, то в сукупності з вищеописаним властивостями можна зробити висновок, що радіус дорівнює половині висоти ромба. (Ріс.115.3) r = h / 2
Є така формула для площі довільного чотирикутника з діагоналями d₁, d₂, кут між якими φ: S = ½ d₁d₂ sin φ. У разі ромба (кут між діагоналями прямий) це дає S = ½ d₁d₂ = ½ · 14 · 48 = 336. З іншого боку, S = ah, де a - сторона, h - висота ромба. Сторону можна знайти по теоремі Піфагора, розглянувши трикутник-четвертинку ромба: a² = (14/2) ² + (48/2) ² = 49 + 576 = 625 = 25², a = 25. Отже, 336 = S = 25h, звідки h = 13,44 (см). У загальному вигляді: S = ½ d₁d₂ = ah = ½√ (d₁² + d₂²) · h, h = d₁d₂ / √ (d₁² + d₂²). З трапецією все гірше. Тільки через діагоналі (не знаючи ще якогось елементу) площа висловити не вийде. ========== ДОДАВАННЯ Нехай ABCD - трапеція (BC
розглянемо один з прямокутних трикутників ромба, гле два катета рівні половин діагоналей. да катета рівні 7 і 24. тоді сторона ромба по т пифагора дорівнює 25 висота ромба дорівнює 7 * 24/25 - це з прямокутного трикутника: помножити два катета і розділити на гіпотенузу так що висота дорівнює 6,72 ------- ------
площа трапеції, знаючи діагоналі дорівнює 1/2 d1 * d2 * sin (a)? де а - кут між діагоналями. ЦЕ ЯКЩО ТРАПЕЦІЯ равнобокой І діагоналі рівні
Знаючи діагоналі, знайти висоту ромба легко. У цьому нам допоможе теорема Піфагора. І хоч вона стосується прямокутних трикутників, в ромбі вони теж є - їх утворює перетин двох діагоналей d1 і d2:
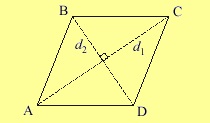
Уявімо, що діагональ 1 дорівнює 30 сантиметрам, а діагональ 2 - 40 см.
Щоб обчислити висоту, нам доведеться порахувати площу ромба і розмір одного катета (в ромбі, як відомо, вони однакові).
Отже, наші дії:
- Підраховуємо величину сторони по теоремі Піфагора. Сторона BC - це гіпотенуза (бо лежить навпроти тупого кута) трикутника BXD (X - це перетин діагоналей d1 і d2). А значить розмір цієї сторони в квадраті дорівнює сумі квадратів сторін BX і XC. Їх розмір нам теж відомий (діагоналі ромба перетином діляться навпіл) - це 20 і 15 сантиметрів. Виходить, що довжина сторони BC дорівнює кореню від 20 у квадраті і 15 в квадраті. Сума квадратів діагоналей дорівнює 625, а якщо витягти це число з кореня, отримуємо розмір катета, дорівнює 25 сантиметрам.
- Обчислюємо площу ромба за допомогою двох діагоналей. Для цього множимо d1 на d2 і ділимо результат на 2. Виходить: 30 помножити на 40 (= 1200) і поділити на 2 - виходить 600 см кв. - це і є площа ромба.
- Тепер обчислюємо висоту, знаючи довжину сторони і площа ромба. Для цього потрібно площа поділити на довжину катета (це і є формула обчислення висоти ромба) 1200 ділимо на 25 - виходить 48 сантиметрів. Це остаточну відповідь.
Як знайти висоту ромба, якщо відома площа і периметр (яка формула)?
Ознайомтеся з усіма формулами розрахунку площі ромба:
Щоб дізнатися висоту, нам потрібна найперша формула (Площа = Висота помножити на Довжину сторони).
Припустимо, що периметр дорівнює 124 см, а площа - 155 см кв.
Нам грає на руку те, що у ромба всі сторони однакові, тому його периметр - це 4 помножити на довжину одного катета.
Щоб підрахувати висоту ромба, потрібно дізнатися розмір катета. Ось які дії допоможуть у вирішення завдання:
- Знайдемо довжину сторони ромба через відомий периметр. Для цього значення периметра (124) ділимо на 4, і отримуємо значення 31 сантиметр - довжина катета.
- Підраховуємо висоту через формулу площі. Ділимо площа (155 см кв.) На розмір катета (31 см) і отримуємо 5 сантиметрів - це розмір висоти даної геометричної фігури.
Як знайти висоту ромба, якщо відома сторона і кут?
Завдання здається складною, але це не так. Уявімо, що розмір катета ромба дорівнює кореню з трьох, а кут - 90 градусів.
Щоб порахувати розмір висоти, використовуємо формулу площі ромба (сторона в квадраті помножити на синус кута). Щоб дізнатися синус будь-якого градуса, скористайтеся в моїй обороні. Синус 90 градусів дорівнює 1, тому знайти висоту буде дуже просто. Виходить, що площа дорівнює квадрату довжини сторони (3) помножити на синус 90 гр. (1), що в підсумку дає відповідь-3 см кв.
А потім ділимо отриману площу на розмір катета: 3 поділити на корінь з 3, і отримуємо висоту ромба -√3.
Як порахувати висоту ромба, якщо відома сторона і діагональ?
У цьому завданні потрібно використовувати прямокутний трикутник, який утворений перетином діагоналей.
Припустимо, що сторона дорівнює 10 см, а діагональ - 12 см.
- Знаходимо розмір половини другої діагоналі за допомогою теореми Піфагора. Гіпотенуза в нашому випадку - це сторона, тому величина половини діагоналі буде дорівнює різниці квадрата катета (10 в квадраті) і квадрата половини відомої діагоналі (6 в квадраті). Виходить, що потрібно від 100 відняти 36 - маємо 64 сантиметри. Видобуваємо корінь з цього числа і отримуємо довжину половини другої діагоналі - 8 см. А повна довжина дорівнює 16 сантиметрам.
- Підраховуємо площа ромба за допомогою двох діагоналей. Множимо довжину першої діагоналі (12 см) на довжину другої (16 см) і ділимо це на 2 - отримуємо 96 см кв. (Це площа ромба).
- Обчислюємо висоту, знаючи розмір сторони і площа. Для цього 96 поділіть на 10 - виходить 9,6 сантиметрів - це остаточна відповідь.
Рекомендую ще почитати про