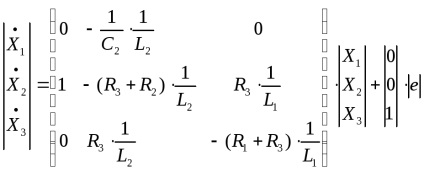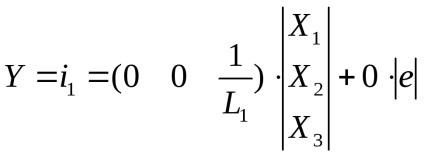Яка Формує фільтр - лінійна стаціонарна система, яка при вхідному сигналі, у вигляді білого шуму, формує на виході випадковий процес X (t) з заданими статистичними характеристиками.
Для визначення передавальної функції формує фільтра скористаємося рівнянням (17):
.
дріб
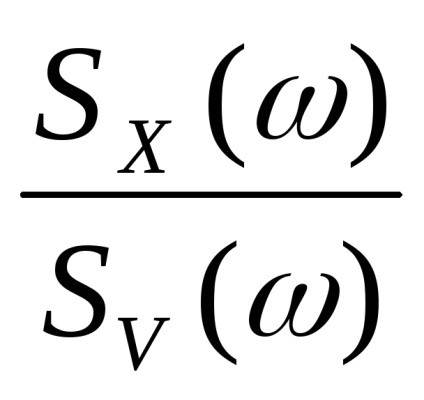
Таким чином, квадрат модуля частотної характеристики можна буде представити у вигляді:
,
де
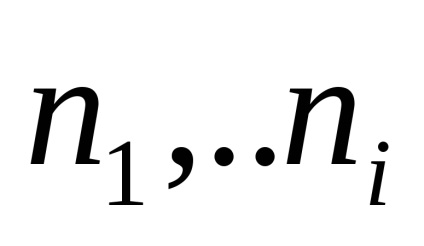
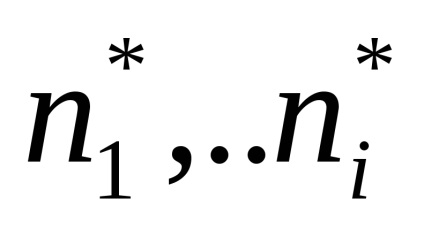

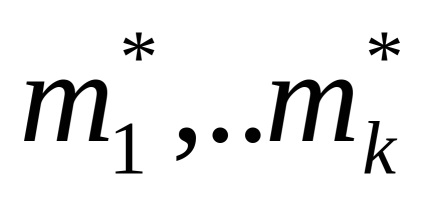
Помітивши, що коріння попарно комплексно-зв'язані (тобто
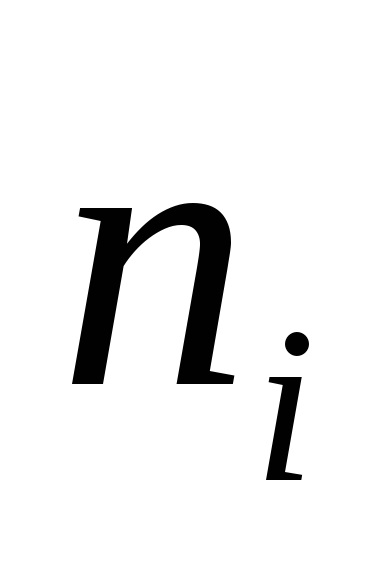
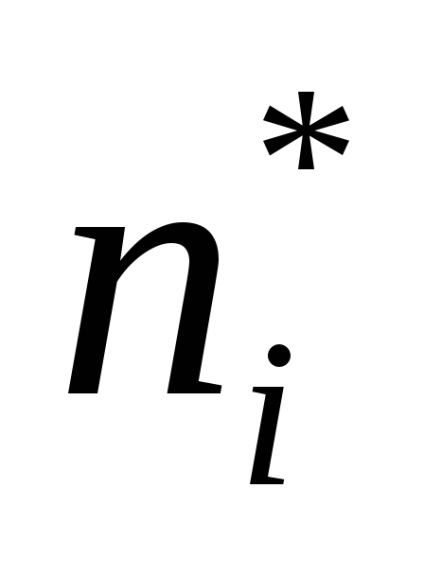
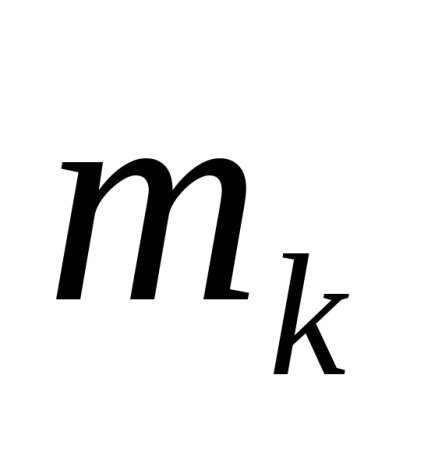
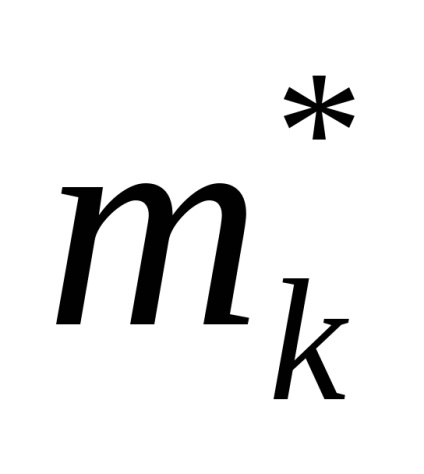
,
.
Таким чином, для формування вираження передавальної функції формує фільтра
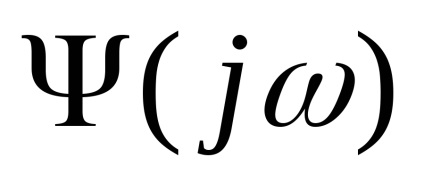
Кореляційна функція, спектральна щільність стаціонарного процесу, характеристики білого шуму
Стаціонарний процес - випадковий процес, що не змінює своїх характеристик з плином часу, і все n -мірні функції розподілу ймовірності не змінюються в залежності від зміни початку відліку часу.
Стаціонарна кореляційна функція - випадкова функція з постійним математичним очікуванням і коефіцієнтом кореляції, що залежать від різниці аргументів.
.
Спектральна щільність стаціонарного випадкового процесу X (t) - частотна функція, що характеризує спектральний склад процесу і визначається виразом:
Зв'язок між спектральної щільністю і кореляційної функцією:
.
Білий шум - стаціонарний випадковий процес, який має постійну спектральну щільність.
.
У випадкового процесу типу білого шуму завжди відсутній зв'язок між попередніми та наступними реалізаціями. У зв'язку з цим кореляційна функція білого шуму має вигляд:
.
Кореляційна функція білого шуму з точністю до const є δ-функцію - певний імпульс:
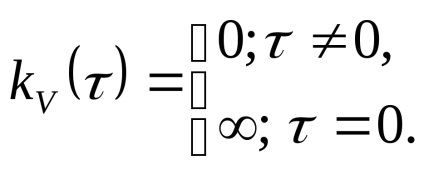
Білий шум - стаціонарний випадковий процес, у якого перетином є некорельовані випадкові величини з нескінченними дисперсиями:
.
Розрізняють інтенсивність білого шуму, в цьому випадку його розглядають як нестаціонарний випадковий процес:
,
де
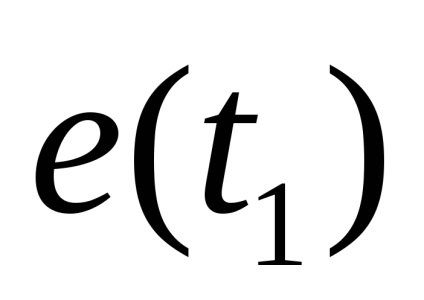
Побудови математичної моделі для електричної схеми
Розглянемо приклад побудови математичної моделі в просторі станів для об'єкта управління, представленого у вигляді електричної схеми (рис. 3.)
Рис.3. Електрична схема об'єкта управління
Об'єкт управління заданий у вигляді електричної схеми та для переходу до математичного опису об'єкта слід записати за другим законом Кірхгофа рівняння для всіх контурів. І знайти систему рівнянь, що описує-вающий об'єкт управління за методом контурних струмів. В якості вихідної величини використовується струм в першому контурі i1.
Для переходу до математичного опису об'єкта запишемо за другим законом Кірхгофа рівняння для всіх контурів, і знайти систему рівнянь, що описує-вающий об'єкт управління за методом контурних струмів. У нашому випадку:
У вихідній системі рівнянь слід позбутися всіх інтегралів, продифференцировав рівняння.
Позбавляються від інтеграла в останньому рівнянні:
Використовуючи метод умовного інтегрування, слід ввести фіктивні змін-ні, рівні елементам, узятим з рівнянь, але на 1 або більше порядків нижче.
У нашому випадку, використовуючи метод умовного інтегрування, вводимо фіктивні змін-ні, рівні елементам, узятим з рівняння (22) на 1 і 2 порядки нижче і з першого рівняння системи (21).
Знаходяться похідні за часом від фіктивних змінних і, застосовуючи попередні рівняння, виражаються залежностями від струмів і фіктивних змінних.
Для даного випадку:
Із системи (23) (і при необхідності (21)) виражаються струми таким чином щоб вони залежали тільки від фіктивних змінних.
Із системи (23) вирази для струмів через фіктивні змінні запишеться у вигляді:
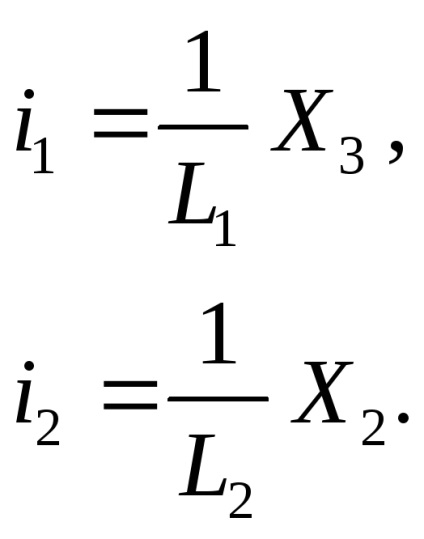
Отримані вирази струмів підставляються в систему (24) і система доповнюється виразом для вихідної величини, в результаті отримують.
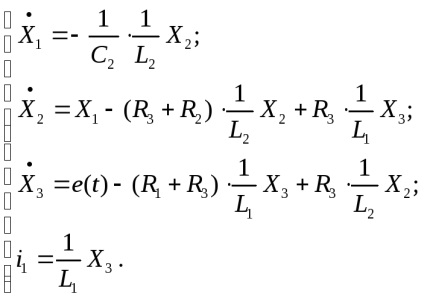
За отриманою системі рівнянь і рівняння для вихідної величини об'єкта регулювання записується математична модель в нормальної фор-ме Коші:
- рівняння вихідної величини об'єкта.
де А, В, С, D - матриці, X - матриця внутрішніх змінних, U - матриця вхідних змінних, в даному випадку U - ЕРС.
В даному випадку матриці матимуть вигляд:
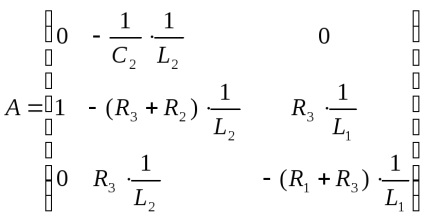
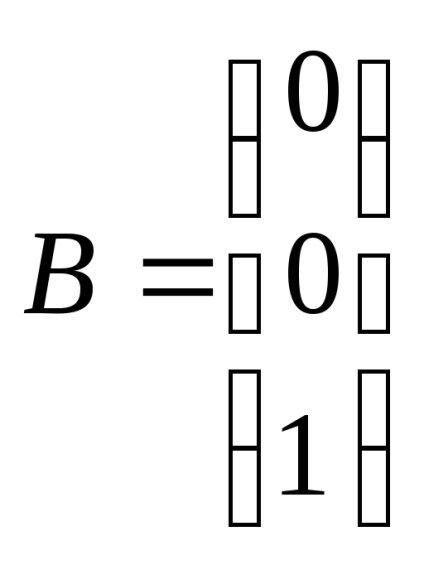
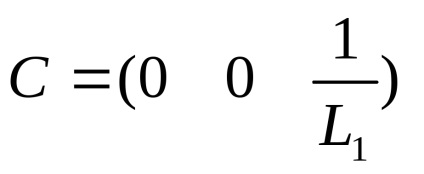
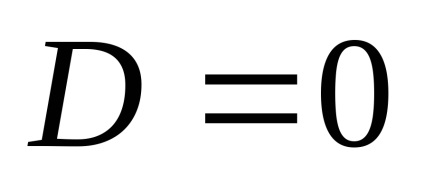
Отримуємо математичну модель в просторі станів: