Які моменти інерції називаються власними

Осьові і відцентрові моменти інерції щодо осей, що проходять через центр ваги поперечного перерізу стержня, іноді називаються власними моментами інерції.

За якою формулою обчислюються моменти інерції фігури відносно осі, паралельної центральній? Які моменти інерції називаються переносними?

Нехай дві взаємно перпендикулярні осі x і y проходять через центр ваги C поперечного перерізу стержня. Проведемо інші осі координат

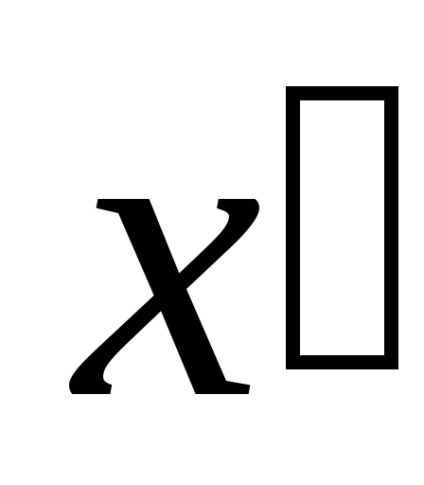
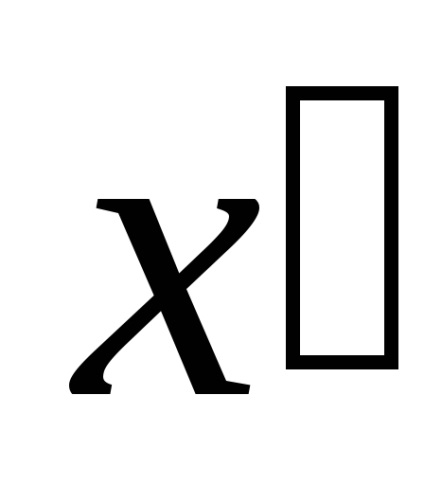
і, паралельні осямx і y. Позначимо a і b координати центру ваги З в нових осях і(Рис. 4.3, а).

Т

оли осьові і відцентрові моменти інерції фігури відносно нових осейівизначатимуться за такими формулами:

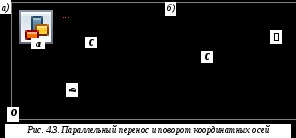
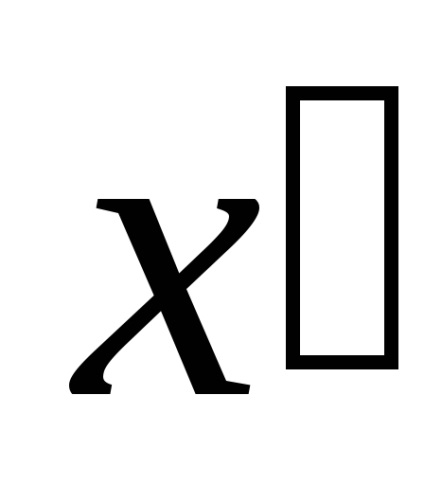
Перші доданки в цих формулах раніше нами були названі власними моментами інерції. Другі (підкреслені) складові у формулі (4.6) називаються переносними моментами інерції.

Відзначимо, що координати a і b необхідно підставляти в формули (4.6) з урахуванням їх знаків. що є вкрай важливим для третьої з цих формул.

Як змінюються власні моменти інерції при повороті координатних осей?

Нехай нам відомі власні моменти інерції

,іщодо двох взаємно перпендикулярних осейx і y. проходять через центр ваги C поперечного перерізу стержня. Проведемо через точку C інші осі і, повернені щодо осейx і y на кут (Рис. 4.3, б). Будемо вважати цей кут позитивним, якщо поворот осей відбувається проти годинникової стрілки.

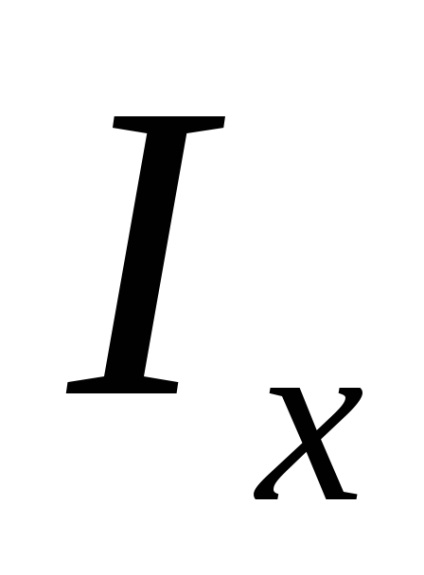
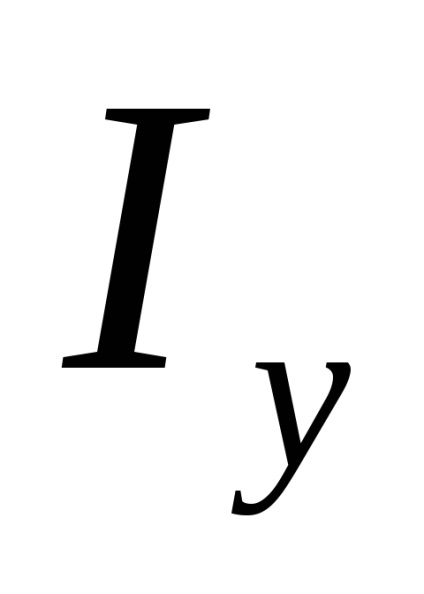
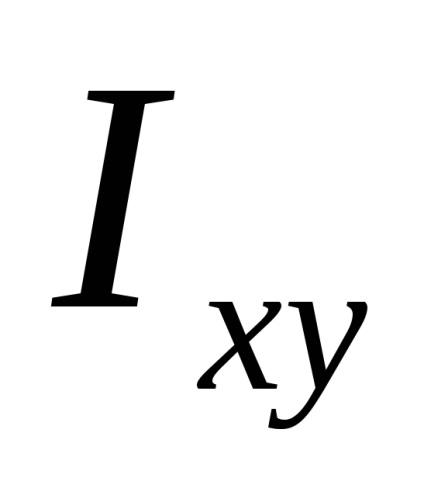
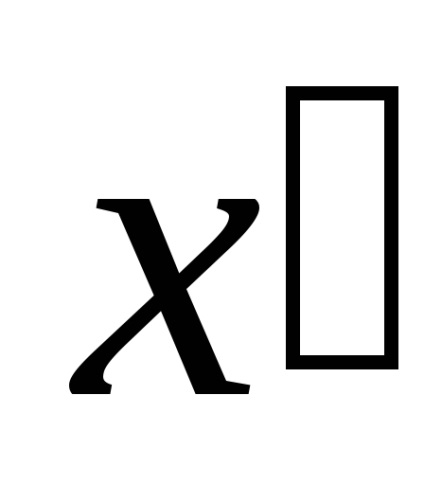
Тоді моменти інерції поперечного перерізу відносно новихосей визначаються за формулами:

;

.

З формул (4.7) видно, що

,

тобто сума власних осьових моментів інерції є величиною постійною (вона не змінюється при повороті координатних осей).

Як вже зазначалося вище, дві взаємно перпендикулярні осі, що проходять через центр ваги фігури, щодо яких відцентровий момент інерції дорівнює нулю, називаються головними центральними осями інерції. тоді при

з третьої формули (4.7) після нескладних перетворень можна визначити напрямки цих осей:

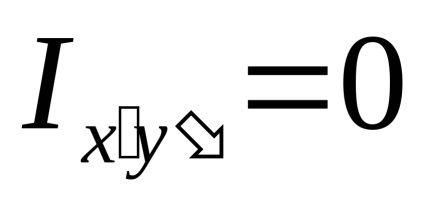
З отриманого виразу (4.8) ми знайдемо два значення кута

, які відрізняються один від одного на кут. Вони і визначають положення двох головних центральних осей.

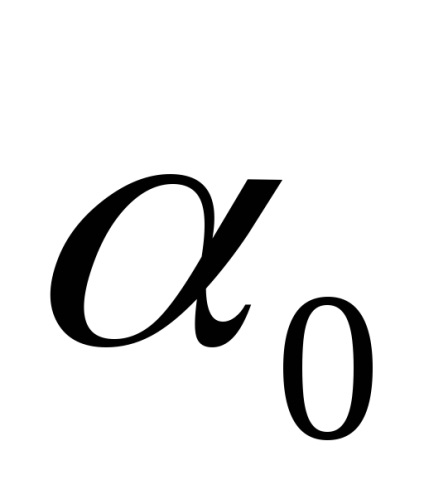
Які власні осьові моменти інерції називаються головними моментами інерції?

При повороті центральних осей і наближенні їх до головних центральним осях, більший з власних осьових моментів інерції стає ще більше, прагнучи до свого максимального значення

,а менший - ще менше. наближаючись до мінімального значення .

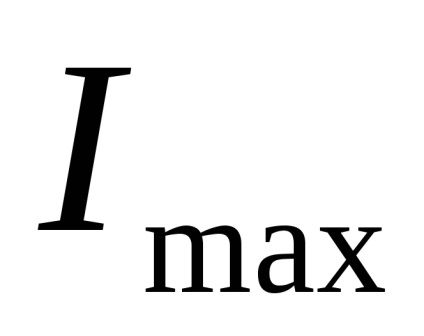
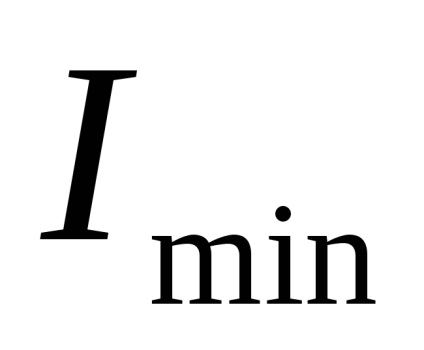
Моменти інерції фігури відносно головних центральних осей

і називаютсяглавнимі центральними моментами інерції. Вони можуть бути обчислені за наступними формулами:

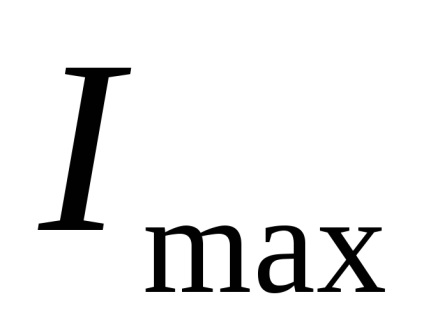
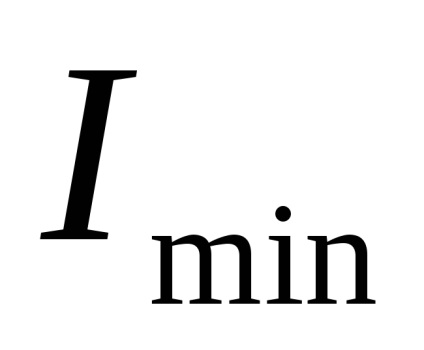
Відзначимо важливе властивість, що з цих формул. Якщо в окремому випадку

, то осьові моменти інерціїітеж рівні між собою і при повороті осей взагалі не змінюються. Тоді будь-які дві взаємно перпендикулярні осі, що проходять через центр ваги поперечного перерізу, є головними центральними осями.

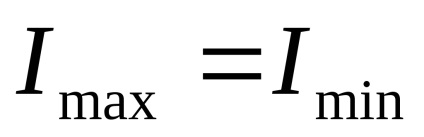
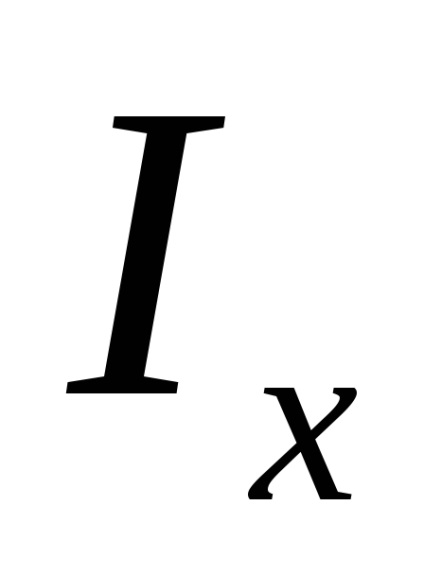
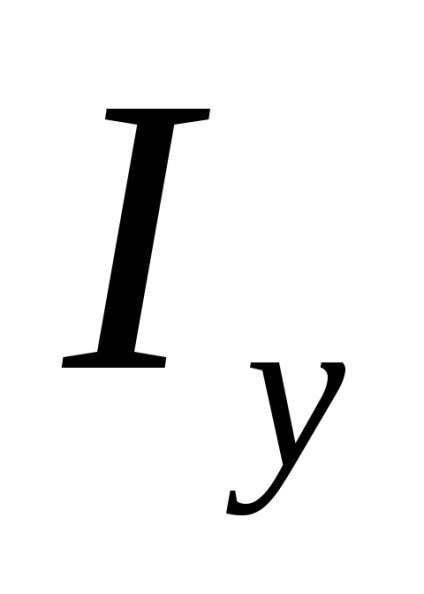
Як для складної фігури визначити, яка з головних центральних осей є віссю max, тобто тією віссю, щодо якої момент інерції приймає найбільше значення?

За визначенням осьової момент інерції дорівнює інтегралу творів елементарних майданчиків на квадрат їх відстаней до відповідної осі. Тому, чим більше майданчики віддалені від осі і чим більше таких майданчиків, тим більше і осьової момент інерції.

Схожі статті

• Яка частина мови називається іменником в російській мові

• З якого моменту чоловік - власність жінки

• Який хрестик для хрещення немовляти краще вибрати