КАРТОГРАФІЧНІ ПРОЕКЦІЇ, математичні методи відображення всієї поверхні земного еліпсоїда або його частини на площині карти. Картографічні проекції встановлюють відповідність між геодезичними координатами точок (широтою В і довготою L) і їх прямокутними координатами (Х і У) на карті:
Конкретні реалізації функцій f1. і f2 часто складні, їх число нескінченно, і, отже, різноманітність картографічних проекцій необмежено. Вихідна аксіома картографічних проекцій полягає в тому, що сферичну поверхню не можна розгорнути на площину без деформацій - стиснень і розтягувань, різних за величиною і напрямком. Математична картографія вивчає всі види спотворень і розробляє методи побудови проекцій, в яких спотворення мали б або найменші (в будь-якому сенсі) значення, або заздалегідь заданий розподіл. Різні картографічні проекції можуть мати такі види спотворень: спотворення довжин - масштаб довжин і відстаней непостійний в різних точках карти і за різними напрямками; спотворення площ - масштаб площ в різних точках карти різний, що порушує розміри об'єктів; спотворення кутів - кути між напрямами на мапі спотворені щодо кутів на місцевості; спотворення форм - фігури на карті деформовані і не подібні фігурам на місцевості, що є наслідком спотворення кутів.
У будь-картографічної проекції розрізняють головний масштаб довжин і площ - відношення, що показує ступінь зменшення розмірів еліпсоїда (кулі) щодо його зображення на карті, і приватні масштаби - відношення нескінченно малого відрізка (або площі), зображеного на карті, до відповідної нескінченно малій величині на еліпсоїді (кулі). Картографічні анімації мають ще й тимчасової масштаб, т. Е. Ставлення часу демонстрації карти до реального часу зображуваного процесу.
За характером спотворень, що виникають при переході від сферичної поверхні до площини, картографічні проекції поділяють на рівновеликі, які зберігають розміри площ, рівнокутні, залишають без спотворень кути і форми контурів (раніше їх називали конформними), і довільні, де площі і кути спотворені в різних співвідношеннях. Окремий випадок довільних картографічних проекцій - равнопромежуточние проекції, в яких масштаб постійний по одному з головних напрямків (по меридіану або паралелі). Дивись карти картографічній проекції.
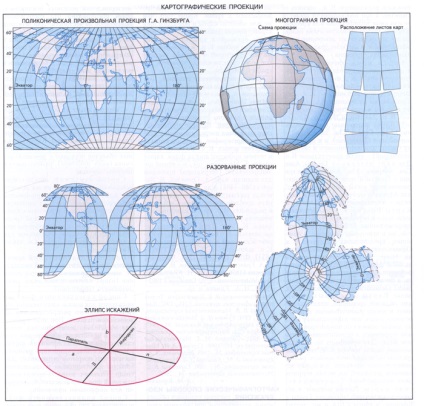
Мірою деформацій в картографічній проекції служить еліпс спотворень (або індікатріса Тіссо). Будь-яка нескінченно мала окружність на земній кулі (еліпсоїді) постає на мапі нескінченно малим еліпсом, розміри і форма якого відображають спотворення довжин, площ і кутів. Довжина і орієнтування великий осі еліпса спотворень відповідають напрямку найбільшого розтягування (а) в даній точці, а мала вісь - найбільшого стиснення (b), відрізки вздовж меридіана і паралелі характеризують приватні масштаби вздовж них (m і n).
Спотворення на картах можна також показувати за допомогою особливих изолиний - ІЗОКОЛ, т. Е. Ліній рівних спотворень довжин, площ, кутів або форм.
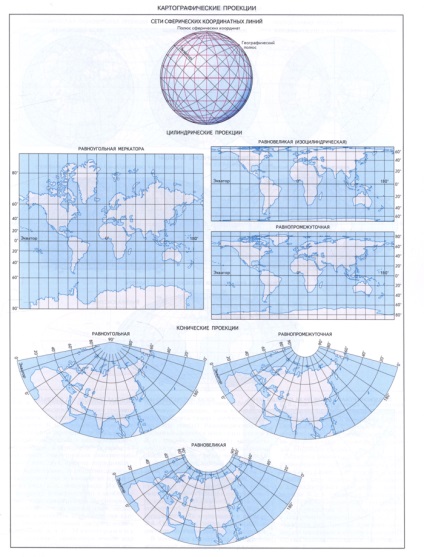
Залежно від положення осі, використовуваної при проектуванні системи сферичних координат, розрізняють картографічні проекції нормальні (вісь сферична координат збігається з віссю обертання Землі), поперечні (вісь сферичних координат лежить в площині екватора) і косі (вісь сферичних координат розташована під кутом до площини екватора ).
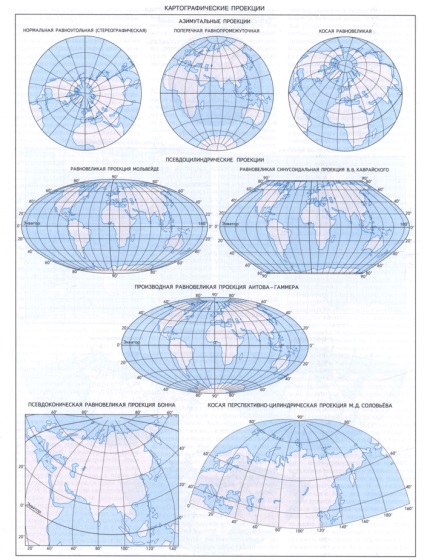
По виду нормальної сітки меридіанів і паралелей виділяють циліндричні картографічні проекції, в яких меридіани і паралелі нормальної сітки є прямими, взаємно перпендикулярними лініями; інакше кажучи, земну кулю (еліпсоїд) як би проектують на допоміжну поверхню дотичного або колія циліндра, який потім розгортають у площину. У конічних картографічних проекціях поверхню земної кулі також проектують на допоміжну поверхню дотичного або колія конуса, тому в нормальної конічної проекції меридіани - це прямі, що виходять з точки полюса, а паралелі - дуги концентричних кіл. У нормальних (полярних) азимутальних картографічних проекціях поверхню земної кулі переносять на допоміжну площину, перпендикулярну осі обертання Землі, паралелі в ній - концентричні кола, а меридіани - діаметри цих кіл. У цій проекції завжди картографують полярні області. Якщо площину проекції перпендикулярна до площини екватора, то виходить поперечна (екваторіальна) азимутальная проекція, яку завжди використовують для карт півкуль. Допоміжні дотичні поверхні дають одну загальну лінію або точку для еліпсоїда (кулі) і площині карти, де спотворення відсутні. У разі січною поверхні з'являються дві загальні лінії. У псевдоціліндріческіх картографічних проекціях паралелі - прямі (як і в циліндричних проекціях), середній меридіан - перпендикулярна їм пряма, а решта меридіани - криві, що збільшують кривизну в міру віддалення від середнього меридіана. У псевдоконіческіх картографічних проекціях все паралелі постають дугами концентричних кіл (як в нормальних конічних), середній меридіан - пряма лінія, а решта меридіани - криві, причому кривизна їх зростає з віддаленням від середнього меридіана. У нормальних поліконічній картографічних проекціях паралелі представлені дугами ексцентричних кіл, а меридіани - кривими, симетричними щодо прямого середнього меридіана. Полярні псевдоазімутальние картографічні проекції - це видозмінені азимутальні проекції, в яких паралелі зображені у вигляді концентричних кіл, а меридіани - у вигляді кривих ліній, симетричних відносно одного або двох прямих меридіанів.
Комп'ютерні технології дозволяють отримувати ці та безліч довільних картографічних проекцій будь-якого виду. Їх властивості задають відповідно до особливостей картографуванню території і її положенням на земній кулі, призначенням і способом використання карти, кращим розподілом спотворень і т.п. Багатогранні картографічні проекції отримують, проектуючи земну кулю на поверхню багатогранника. Найчастіше кожна грань являє собою равнобочной трапецію, хоча можливі й інші варіанти (наприклад, шестикутники, квадрати, ромби). Різновидом багатогранних є багатосмугові картографічні проекції, причому смуги можуть «нарізатися» по меридіанах і паралелями. Такі проекції зручні тим, що спотворення в межах кожної грані або смуги невеликі, тому їх завжди використовують для багатолистий карт. Топографічні та оглядово-топографічні карти створюють виключно в багатогранної проекції, і рамка кожного листа є сферичну трапецію, утворену лініями меридіанів і паралелей. Однак блок листів карт можна поєднати із загальних рамок без розривів.
Численність картографічних проекцій пояснюється різноманітністю завдань, для яких служать карти (наприклад, для морських і аеронавігаційних карт потрібні рівнокутні, а для кадастрових вимірювань - рівновеликі картографічні проекції), географічним положенням території (полярні області зображують в нормальних картографічних проекціях, а півкулі - в поперечних азимутальних картографічних проекціях), призначенням карт (різні проекції потрібні для шкільних і науково-довідкових карт). Створено спеціальні електронні атласи картографічних проекцій, за допомогою яких можна знайти потрібну картографічну проекцію, оцінити її властивості, а при необхідності провести ті чи інші модифікації або перетворення. Вибір варіантів дуже великий, але все ж існують деякі кращі і найбільш традиційні картографічні проекції.
Карти світу зазвичай складають в циліндричних, псевдоціліндріческіх і поліконічній картографічних проекціях. Для зменшення спотворень часто використовують січні циліндри, а псевдоціліндріческіе картографічні проекції дають з розривами на океанах. Карти півкуль завжди будують в азимутальних картографічних проекціях. Для Західного і Східного півкуль використовують поперечні (екваторіальні), для Північного і Південного півкуль - нормальні (полярні), а в інших випадках (наприклад, для материкового і океанічних півкуль) - косі азимутальні картографічні проекції. Для карт материків Європи, Азії, Північної Америки, Південної Америки, Австралії з Океанією найчастіше застосовують рівновеликі косі азимутальні картографічні проекції, для Африки - поперечні, а для Антарктиди - нормальні азимутальні картографічні проекції. Карти Росії в цілому складають найчастіше в нормальних конічних равнопромежуточних картографічних проекціях з січним конусом, але в деяких випадках - в поліконічній, довільних і в інших картографічних проекціях. Однак сітка конічних картографічних проекцій не завжди зручна. Наприклад, на картах Росії для початкової школи потрібно картографічна проекція, в якій меридіани сходяться в точці полюса, а сама північній точка суші (мис Челюскін) розташовується ближче всього до північної рамці. Карти окремих країн, адміністративних областей, провінцій, штатів виконують в косих рівнокутних і рівновеликих конічних або азимутальних картографічних проекціях, але багато що залежить від конфігурації самої території та її положення на земній кулі. Для невеликих за площею районів завдання вибору картографічних проекцій втрачає актуальність, можна використовувати різні рівнокутні проекції, оскільки спотворення площ на малих територіях малоощутіми. Топографічні карти Росії створюють в поперечно-циліндричної проекції Гаусса - Крюгера, а карти США і багатьох інших західних країн - в універсальній поперечно-циліндричної проекції Меркатора (скорочено UTM). Обидві проекції близькі за своїми властивостями, і та і інша по суті є багатосмуговими. Морські і аеронавігаційні карти виконують виключно в циліндричної проекції Меркатора, а тематичні карти морів і океанів створюють в найрізноманітніших, інколи досить складних проекціях. Наприклад, для спільного показу Атлантичного і Північного Льодовитого океанів застосовують особливі проекції з овальними Ізокол, а для зображення Світового океану - рівновеликі проекції з розривами на материках.
У будь-якому випадку при виборі проекції, особливо для тематичних карт, слід мати на увазі, що зазвичай спотворення на мапі мінімальні в центрі і швидко зростають до країв. Крім того, чим дрібніше масштаб карти і ширше просторовий охоплення, тим більша увага доводиться приділяти математичним факторів вибору картографічних проекцій, і, навпаки, для малих територій і великих масштабів більш істотними стають географічні чинники.
Короткі історичні відомості. Перші карти з використанням сітки меридіанів і паралелей створили грецькі вчені Ератосфен, Гіппарх. Клавдій Птолемей в «Керівництві з географії» описав принципи створення деяких конічних проекцій. Великі географічні відкриття послужили значному розвитку картографії і сприяли створенню нових картографічних проекцій. Великий внесок у теорію проекцій внесли фламандські картографи: Г. Меркатор, який запропонував циліндричну (Меркатора) проекцію для навігаційних карт, А. Ортелій, Я. Янсон (1588-1664) та ін. Теорія проекцій завжди розглядалася як найважливіша наукова проблема картографії. Свій внесок в розробку картографічних проекцій внесли відомі математики І. Ламберт, Л. Ейлер, Ж. Лагранж, К. Гаусс. В середині 19 століття французький дослідник А. Тіссо створив загальну теорію спотворень картографічних проекцій. У Росії теорією картографічних проекцій займалися А. П. Болотов (1803-1853), Ф. І. Шуберт, П. Л. Чебишев, Д. А. Граве, Д. І. Менделєєв, В. В. Вітковський (1856-1924 ), Ф. Н. Красовський, В. В. Каврайський, Г. А. Гінзбург (1905-1975), Н. А. Урман і ін.