Кінетичної енергією системи називається скалярна величина Т, що дорівнює арифметич-ської сумі кінетичних енергій всіх точок системи
Кінетична енергія є характеристикою і поступателен-ного і обертального руху системи, тому теоремою про изме-нении кінетичної енергії особливо часто користуються при вирішенні завдань.
Якщо система складається з декількох тіл, то її кінетична енергія дорівнює, очевидно, сумі кінетичних енергій цих тел:
Кінетична енергія - скалярна і завжди позитивна величина.
Знайдемо формули для обчислення кінетичної енергії тіла в різних випадках руху.
1. Поступальний рух. В цьому випадку всі крапки тіла рухаються з однаковими швидкостями, рівними швидкості дви-жения центру мас. Тобто, для будь-якої точки Vi = VC
Таким чином, кінетична енергія тіла при поступателен-ном русі дорівнює половині твори маси тіла на квад-рат швидкості центру мас. Від напрямку руху значення Т не залежить.
2. Обертальний рух. Якщо тіло обертається навколо якоїсь осі Оz (див. Рис.1), то швидкість будь-якої його точки де - відстань точки від осі обертання, а - угло-вая швидкість тіла. Підставляючи це значення і виносячи загальні множники за дужки, отримаємо:
Величина, що стоїть в дужках, являє собою момент інерції тіла відносно осі z. Таким чином, остаточно знайдемо:
тобто кінетична енергія тіла при обертальному русі дорівнює половині твори моменту інерції тіла щодо осі обертання на квадрат його кутової швидкості. Від напрямку обертання значення Т не залежить.
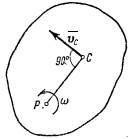
При обертанні тіла навколо нерухомої точки кінетична енергія визначається як (рис.2)
де - моменти інерції тіла відносно головних осей інерції x1. y1. z1 в нерухому точку О; - проекції вектора миттєвої кутової швидкості на ці осі.
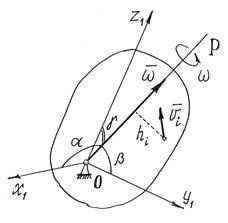
3. плоскопаралельному рух. При цьому руху-ванні швидкості всіх точок тіла в кожен момент часу распреде-лени так, як якщо б тіло оберталося навколо осі, перпендикулярної до площини руху і проходить через миттєвий центр ско-зростання Р (рис.1). отже
де - момент інерції тіла відносно названої вище осі, - кутова швидкість тіла. Величина у формулі буде змін-ної, так як положення центру Р при руху-ванні тіла весь час змінюється. Введемо замість постійний момент інерції, щодо осі, що проходить через центр мас С тіла. По теоремі Гюйгенса-Штейнера, де d = PC. Підставами цей вислів для. З огляду на, що точка Р - миттєвий центр швидкостей, і, отже,, де - швидкість центру мас С. остаточно знайдемо:
Отже, при плоскопаралельному русі кинетич-ська енергія тіла дорівнює енергії поступального руху зі швидкістю центру мас, сло-женной скінетіческой енергією обертального руху навколо центру мас.
4) Для самого загального випадку руху матеріальної системи кінетичну енергію допомагає обчислити теорема Кеніга.
Розглянемо рух матеріальної системи як суму двох рухів (рис.3). Переносного - поступального руху разом з центром мас С і відносної - руху щодо поступально рухомих разом з центром мас осей x1, y1, z1. Тоді швидкість точок. Але переносний рух - поступальний. Тому переносні швидкості всіх точок рівні, рівні. Значить, і кінетична енергія буде
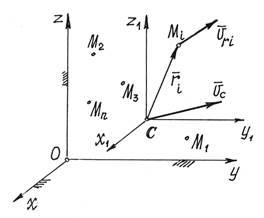
За визначенням центру мас його радіус-вектор в рухомий системі (центр мас знаходиться на початку координат), значить, і. Похідна за часом від цієї суми також дорівнює нулю:
Тому, звичайно, кінетична енергія системи
Кінетична енергія матеріальної системи дорівнює сумі кінетичної енергії при поступальному русі разом з центром мас і кінетичної енергії її при русі щодо координатних осей, поступально рухомих разом з центром мас.
У загальному випадку руху тіла, яке можна розглядати як суму двох рухів (переносного - поступального разом з центром мас С і відносної - обертання навколо точки С), по теоремі Кеніга (1) отримаємо
де Ix. Iy. Iz - головні центральні осі інерції тіла.