Перші автомобільні і залізні дороги мали вигляд прямолінійних ділянок, з'єднаних дугами кіл. Але коли автомобілі і потяги почали рухатися на більш високих швидкостях, при в'їзді на криволінійні ділянки виникав незручний і небезпечний поштовх. Інженери почали шукати вирішення проблеми і знайшли його в математиці і фізиці. Хочете просте пояснення, чому в якості перехідної кривої використовується клотоїда?
Уявіть, що ви повинні спроектувати шосе або високошвидкісну залізницю. Ви, звичайно, будете намагатися, щоб вона була якомога більш прямий, але повинні будуть з'явитися і деякі криволінійні ділянки. Так як найпростішої кривої з усіх є окружність, то найлегше прямі ділянки з'єднати між собою дугами кіл. Щось на зразок стрічки транспортера.
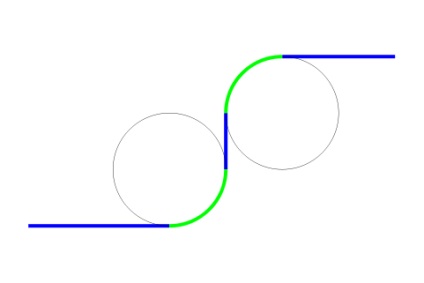
Здається, що такими були перші креслення, і так як перші автомобілі і потяги не рухалися дуже швидко, все йшло гладко. Але все змінилося, коли транспортні засоби змогли досягти більш високих швидкостей. При вході в криволінійні ділянки, на стиках між секціями, з'явився раптовий поштовх. Кепські справи.
Так інженери почали вивчати, в чому справа, і як це можна виправити. Відповідь проста для розуміння і вимагає знання тільки двох речей. Перша йде з геометрії - це радіус кривизни, поняття досить інтуїтивне.
Для кола радіус кривизни - просто радіус кола. Для прямої можна вважати, що це дуууже велика окружність, окружність нескінченного радіуса. Таким чином, радіус кривизни прямий буде нескінченним. Легко, чи не так?
Друге поняття фізичне - це відцентрова сила, яка є ще більш інтуїтивно зрозумілою, хоча суть цього поняття набагато складніше, ніж здається.
Ви, звичайно ж, знаєте, що сила - це "маса, помножена на прискорення '' і, спрощуючи трохи, відцентрова сила має такий вигляд (не лякайтеся, далі йде формула, але вона єдина, і вона нескладна):
де - маса, - швидкість і - наш друг, радіус кривизни.
З одного боку, у нас є маса і швидкість, які перемножуються в цій формулі. Таким чином, чим вони більші, тим більше відцентрова сила. Це зрозуміло: якщо ви рухаєтеся швидше, відцентрова сила буде більше, також вона буде більше, якщо ваша маса більше.
З іншого боку, у нас є радіус кривизни, який стоїть в знаменнику. Таким чином, збільшивши радіус, можна зменшити відцентрову силу. Це зрозуміло: радіус кривизни прямий нескінченний, так що ( "ділячи на нескінченність '') при русі по прямій відцентрова сила дорівнює нулю. Ви також знаєте, що при русі з однієї і тієї ж швидкістю відцентрова сила менше на більш "відкритою '' кривої (з більшим радіусом), ніж на інший" більш закритою '' кривої (з меншим радіусом).
Що тут можна зробити? Подивимося на формулу. маємо
масу, на яку множимо. Для її зменшення необхідно знизити масу автомобіля / поїзда і його пасажирів ... ви добре знаєте, що це не так просто зробити.
Швидкість, на яку множимо (і до того ж в квадраті). Можна їхати повільніше, але тоді це займе більше часу ... і, звичайно, навряд чи це комусь сподобається.
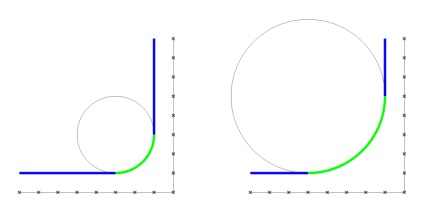
Радіус кривизни, на який ділимо. Для прямої він дорівнює нескінченності, ви не можете його змінити. Так ви могли б збільшити радіус кола, але тоді (як на малюнку вище) відрізки прямих стануть коротшими ... і це точно нікому не сподобається.
Таким чином, потрібно подумати про іншу можливість. Чи можете ви здогадатися, про яку?
Звичайно, можна ввести перехідну криву між прямою і колом. Також було б здорово, щоб при цьому переході радіус кривизни плавно зменшувався від нескінченності (або дуууже великого числа) для прямої до радіуса кола.
Відповідно до формули, відцентрова сила тоді буде змінюватися плавно, а не різко.
Таким чином, вам хотілося б, щоб радіус кривизни зменшувався в міру збільшення відстані? Хвилиночку. Є дві величини ... хочеться, щоб одна ставала менше в той час як інша стає більше ... Це те, що в школі називають обернено пропорційними величинами!
Тобто ви хочете, щоб радіус кривизни і пройдений шлях були обернено пропорційні. І
Що це означає? Ах, так, це означає, що їх твір завжди дорівнює одному й тому числу.
Саме це властивість визначає криву клотоїди, відому математикам і фізикам. Її рівняння має вигляд, (де - постійна, яка взята в квадраті для полегшення побудови кривої).
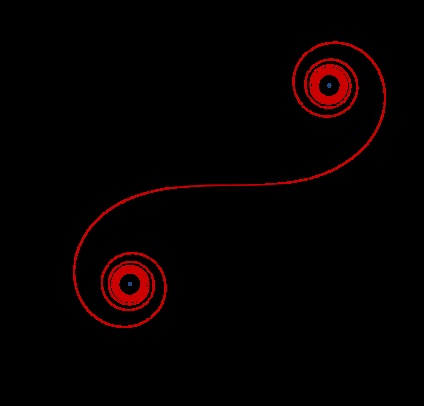
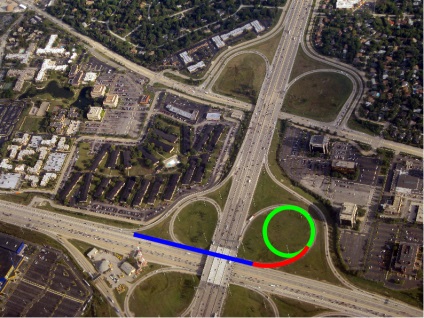
Так що, коли ви їдете по автомобільним і залізницях, ви рухаєтеся, як правило, по прямій - клотоїди - окружності - клотоїди - прямий. Таким чином, відцентрова сила змінюється поступово, і ви можете повертати поступово замість того, щоб робити це різко.
Наступного разу на поворотах згадуйте, що математика і фізика допомагають вам
Все, що сказано вище, відноситься також до переходу з будь-якій кривій на іншу криву.
На додаток до більш-менш звичайним залізних і автомобільних дорогах, клотоїда також використовується на гоночних трасах і американських гірках.

Мабуть, першим вивчати клотоїди почав швейцарський математик Якоб Бернуллі в 1694 році, в контексті задачі теорії пружності. Це завдання було вирішене в 1744 році математиком і фізиком Леонардом Ейлером, який дав характеристику кривої. Приблизно в 1818 р французький фізик Огюстен Жан Френель перевідкрив клотоїди, вивчаючи дифракцию світла, і за допомогою інтегралів отримав параметризацію цієї кривої, еквівалентну параметризації Ейлера. У 1874 році французький фізик Марі Альфред Корню використовував цей вислів, щоб точно побудувати криву. А пізніше, в 1890 році, американський інженер Артур Талбот, ще раз перевідкрив клотоїди в пошуках кривої переходу для залізниць. Якщо ви хочете дізнатися більше про історію клотоїди, ви можете прочитати статтю The Euler spiral: a mathematical history. написану Raph Levien.
Таким чином, клотоїда відома також як спіраль Корню або спіраль Ейлера. Хоча клотоїда виявилася кращою кривої з розглянутими властивостями, також розглядалися й інші можливі перехідні криві, такі як лемніската Бернуллі і овал Кассіні (див. Наприклад, тут: Algunas notas sobre las curvas de las carreteras. 1929 г.).