
Головна | Про нас | Зворотній зв'язок
Розглянемо відокремлений провідник. тобто провідник, який віддалений від інших провідників, тіл і зарядів. Його потенціал прямо пропорційний заряду провідника. З досвіду випливає, що різні провідники, будучи однаково зарядженими, приймають різні потенціали. Тому для відокремленого провідника можна записати
називають електроємна (або просто ємністю) відокремленого провідника.
Ємність відокремленого провідника визначається зарядом, повідомлення якого провіднику змінює його потенціал на одиницю.
Ємність провідника залежить від його розмірів і форми, але не залежить від матеріалу, агрегатного стану, форми і розмірів порожнин всередині провідника. Це пов'язано з тим, що надлишкові заряди розподіляються на зовнішній поверхні провідника. Ємність не залежить також ні від заряду провідника, ні від його потенціалу.
Одиниця виміру електроємна - фарад (Ф): 1 Ф - ємність такого відокремленого провідника, потенціал якого змінюється на 1 В при повідомленні йому заряду в 1 Кл.
Відповідно до формули. потенціал відокремленого кулі радіуса R, що знаходиться в однорідному середовищі з діелектричної проникністю. дорівнює
Використовуючи формулу (8.11.1.), Отримаємо, що ємність кулі
Для того щоб провідник мав велику ємність, він повинен мати дуже великі розміри. На практиці, однак, необхідні пристрої, що володіють здатністю при малих розмірах і невеликих відносно навколишніх тіл потенціалах накопичувати значні по величині заряди, іншими словами, мати великий ємністю. Ці пристрої отримали назву конденсаторів.
Якщо до зарядженого провідника наближати інші тіла, то на них виникають індуковані (на провіднику) або пов'язані (на діелектрику) заряди, причому найближчими до навідних заряду q будуть заряди протилежного знака. Ці заряди, природно, послаблюють поле, створюване зарядом q, тобто знижують потенціал провідника, що призводить (див. (8.11.1.)) до підвищення його електроємна.
Конденсатор - пристрій, що складається з двох провідників (обкладок), розділених діелектриком.
На ємність конденсатора не повинні впливати навколишні тіла, тому провідникам надають таку форму, щоб поле, створюване що накопичуються зарядами, було зосереджено у вузькому зазорі між обкладинками конденсатора. Цій умові задовольняють: 1) дві плоскі пластини; 2) два коаксіальних циліндра; 3) дві концентричні сфери. Тому в залежності від форми обкладок конденсатори поділяються на плоскі, циліндричні та сферичні.
Ємність конденсатора - це фізична величина, що дорівнює відношенню заряду q одного з обкладок, до різниці потенціалів () між його обкладинками:
Розрахуємо ємність плоского конденсатора, що складається з двох паралельних металевих пластин площею S кожна, розташованих на відстані d одна від одної і мають заряди + q і -q. Якщо відстань між пластинами мало в порівнянні з їх лінійними розмірами, то крайовими ефектами можна знехтувати і поле між обкладинками вважати однорідним. Його можна розрахувати, використовуючи формули (8.3.7) і (8.11.4.). При наявності діелектрика між обкладинками різниця потенціалів між ними:
де - діелектрична проникність.
Тоді з формули (8.11.4.), Замінюючи q =. з урахуванням (8.11.5.) отримаємо вираз для ємності плоского конденсатора:
Для визначення ємності циліндричного конденсатора, що складається з двох порожнистих коаксіальних циліндрів з радіусами і (>), вставлених один в іншій, знову нехтуючи крайовими ефектами, вважаємо поле радіально-симетричним і зосередженим між циліндричними обкладинками. Різниця потенціалів між обкладинками обчислимо за формулою для поля рівномірно зарядженого нескінченного циліндра з лінійною щільністю (l - довжина обкладок). З урахуванням наявності діелектрика між обкладинками
Підставивши (8.11.7.) В (8.11.4.), Отримаємо вираз для ємності циліндричного конденсатора:
Для визначення ємності сферичного конденсатора, що складається з двох концентричних обкладок, розділених сферичним шаром діелектрика, використовуємо формулу для різниці потенціалів між двома точками, що лежать на відстанях і (>) від центру зарядженої сферичної поверхні. З урахуванням наявності діелектрика між обкладинками
Підставивши (8.11.9.) В (8.11.4.), Отримаємо
Для збільшення ємності та варіювання її можливих значень конденсатори з'єднують в батареї, при цьому використовується їх паралельне і послідовне з'єднання.
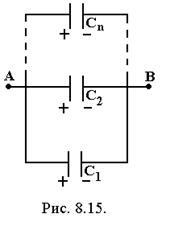
У паралельно з'єднаних конденсаторів різниця потенціалів на обкладках конденсаторів однакова і дорівнює. Якщо ємності окремих конденсаторів. . ...,. то, згідно з (8.11.4.), їх заряди рівні
а заряд батареї конденсаторів
Повна ємність батареї