Прилади й приналежності: металевий балон, рідинний манометр, компресор.
Мета роботи: експериментальне визначення показника адіабати
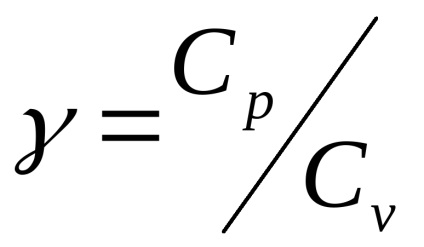
2.1. Теоретична частина
Для характеристики теплових властивостей газу, як і будь-якого іншого тіла, користуються особливою величиною - теплоємністю.
Теплоємністю тіла називають кількість теплоти, яке потрібно підвести до нього або відняти від нього для зміни його температури на 1 К:
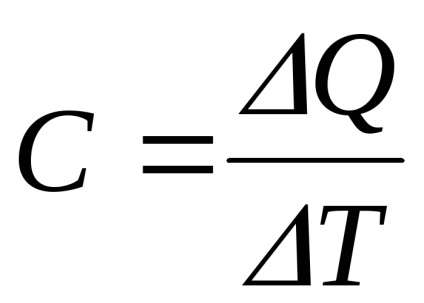
Теплоємність, віднесена до одиниці маси речовини, називається питомою теплоємністю. Вона, очевидно, характеризує вже не тіло, а речовина, з якого це тіло складається. Теплоємність, віднесена до одного молю речовини, називається молярної теплоємністю.
Між питомою теплоємністю - c і молярної - C існує очевидне співвідношення:
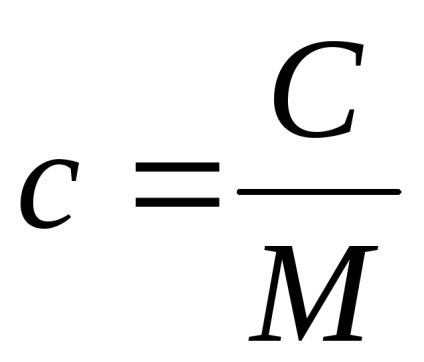
де М - молярна маса (вимірюється в кг / моль).
Теплоємність газу залежить від умов його нагрівання. Зокрема, газ можна нагрівати при постійному обсязі V або при постійному тиску Р. Відповідно отримуємо теплоємність при постійному обсязі Cv і теплоємність при постійному тиску Cp.
Ставлення Сp / Сv = γ є параметром при адіабатних процесах і при процесах, близьких до них (γ називають коефіцієнтом Пуассона).
Процес називається адіабатних, якщо в цьому процесі немає теплообміну газу з довкіллям (стінки судини теплоізольовані). Якщо Адіабатний процес є рівноважним (в кожен момент часу тиск Р і температура Т однакові по всьому об'єму), то він описується рівнянням Пуассона
Відповідно до першого початку термодинаміки
де ΔQ - кількість теплоти, повідомлене газу, ΔU - зміна внутрішньої енергії газу, ΔA - робота, здійснена газом над зовнішніми тілами.
Розглянемо один моль газу. Якщо V = const. то ΔA = 0 і, отже, Сv = ΔU / Т. Якщо Р = const. то ΔA = РΔV = RΔT. так як рівняння стану (PV = RT) справедливо в початковому і кінцевому стані газу.
.
Таким чином, молярні теплоємності Cp і Сv для ідеального газу пов'язані співвідношенням
де R - універсальна газова стала.
Cp> Сv. так як при V = const вся повідомляється газу теплота йде тільки на зміну внутрішньої енергії газу, тоді як при Р = const нагрівання газу неминуче супроводжується його розширенням. При цьому газ здійснює роботу, для чого доводиться повідомляти йому додаткову кількість теплоти.
У молекулярно-кінетичної теорії газів показується, що
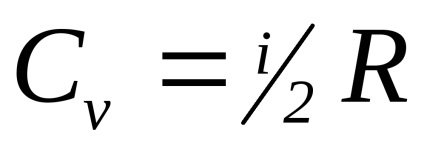
Для одноатомних молекул i = 3 (наприклад, інертні гази), для двох атомної жорсткої молекули (відстань між молекулами постійно) i = 5.
Саме такими є молекули N2 і О2 в повітрі при кімнатних температурах і, отже, для них
.
2.2. Методика визначення коефіцієнта Пуассона
Розглянемо балон з повітрям, герметично закритий поршнем і з'єднаний з рідинним U-подібним манометром (рис 2.1).
1. Нехай спочатку температура повітря в балоні дорівнює кімнатній, а тиск перевищує атмосферний на невелику величину Р '. Рівняння стану повітря в балоні має вигляд
де Р - атмосферний тиск; Т - абсолютна температура газу, що дорівнює температурі навколишнього середовища; V - об'єм, який займає повітрям; Р '- додатковий тиск (визначається по манометру), m - маса повітря в балоні, М - молярна маса повітря (суміш азоту і кисню).
2. Перемістимо поршень вгору. При цьому повітря в балоні розширюється і охолоджується. Зупинимо поршень (в положенні V2) в той момент, коли тиск в балоні стане рівним атмосферному (рівні рідини в обох колінах манометра рівні). При розширенні газ виконує роботу і охолоджується.
Після зупинки поршня повітря в балоні нагрівається до кімнатної температури (за рахунок теплообміну з навколишнім середовищем). при цьому тиск в балоні підвищується на деяку величину P "(Р" <Р'). Уравнение состояния воздуха в баллоне теперь имеет вид
Підкреслимо, що маса повітря в балоні в станах 1 і 2 однакова.
3. У даній роботі істотним є характер переходу повітря в балоні зі стану 1 в стан 2, а саме: якщо розширення повітря відбувається досить швидко, то зміна його внутрішньої енергії значно перевищує енергію, яка встигає за цей час пройти через стінки балона з навколишнього середовища , і процес розширення можна вважати адіабатних. Якщо процес розширення повітря в балоні є рівноважним (тиск і температура однакові по всьому об'єму), то такий процес описується рівнянням Пуассона: РVγ = const. Ясно, що це справедливо тільки при повільному розширенні. При виконанні обох із зазначених умов рівняння Пуассона може бути застосовано і, отже,
де P - атмосферний тиск.
а з (2.1) і (2.2) слід
Порівнюючи (2.4) і (2.5), отримуємо
Логаріфміруя (2.6), маємо
При Р ' «P (при цьому і Р" «P) можна скористатися наближенням ln (1 + x) → x при x → 0. [Переконайтеся за допомогою калькулятора, що при x ≤ 0,02 помилка при заміні ln (1 + x) на x не перевищує 1%. А в даній роботі h ≈ 0,2 м. тоді як атмосферному тиску відповідає висота водяного стовпа h ≈ 10 м].
В результаті отримуємо
так як Р '= ρgh', Р "= ρgh". Таким чином, вимірявши h 'і h ". Можна знайти коефіцієнт Пуассона γ.
2.3. опис установки
Експериментальна установка складається з металевого балона, наповненого повітрям, який з'єднаний з манометром і компресором.
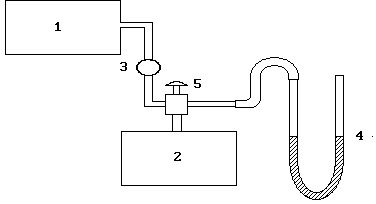
Мал. 2.2. Схема установки:
1 - компресор, 2 - балон, 3 - клапан, 4 - U-подібний манометр, 5 - вентиль
2.4. Порядок виконання роботи
1. За допомогою компресора обережно накачати в балон повітря так, щоб різниця рівнів рідини в манометрі стала рівною 25-30 см. Закрити клапан насоса, почекати 3-4 хвилини, поки температура повітря в балоні не зрівняли з кімнатною (поки рух рівнів в манометрі не припиниться). По нижньому рівню меніска визначити рівні рідини L1 'та L2' в колінах манометра. Занести значення L1 ', L2' і h '= L1' - L2 'в табл. 2.1.
2. За допомогою вентиля з'єднати балон з атмосферою і тримати його відкритим до тих пір, поки рівні в манометрі незрівняються. При цьому аж до вирівнювання кожен рівень повинен рухатися в одну сторону. Після цього закрити вентиль. Повітря в балоні буде нагріватися до кімнатної температури. Відповідно і тиск буде підвищуватися. Через 3-4 хвилини, коли рух рівнів в манометрі припиниться, записати значення L1 ", L2" і h "= L1" -L2 "в табл. 2.1.
Зауваження. При проведенні даного експерименту маса повітря в балоні не залишається постійною. Якщо після накачування (стан 1) його маса m1. то після відкриття крана частина повітря виходить з балона (стан 2), так що маса залишився в ньому повітря m2 Саме дляm2 справедливо все вищесказане при виведенні формули (2.8). Дійсно, в стані 1 маса m2 займає певний обсяг V1 А в стані 2 маса m2 займає вже весь обсяг балона (V2 = V. Рис.2.3). Таким чином, для повітря масою m2 стану 1 і 2 описуються формулами (2.1) і (2.2) відповідно, а перехід 1 → 2 - формулою (2.3). 3. Повторити досліди не менше 10 разів. Результати вимірювань занести в табл. 2.1. 4. За формулою (2.8) розрахувати γ для кожного досвіду. 5. Розрахувати середнє значення γ. 6. Помилку у визначенні γ розрахувати за формулою: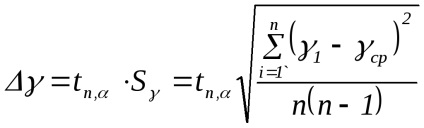
де
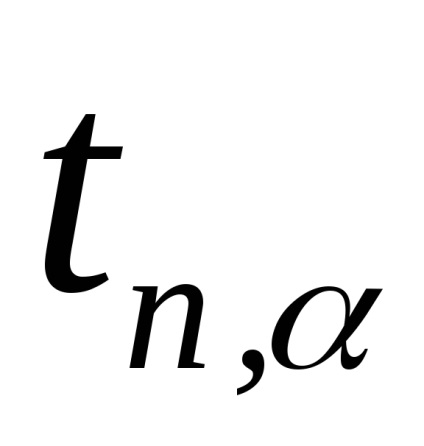
7. Порівняти отримане значення γ = γср + Δγ з теоретичним значенням γ для двоатомних газу.
Як визначаються питома і молярна теплоємності? Який зв'язок між ними? Одиниці виміру.
Від чого залежить теплоємність газів?
Що таке коефіцієнт Пуассона?
Який процес називається адіабатних і яким рівнянням він описується?
Що таке число ступенів свободи молекули?
Чому дорівнює теоретичне значення коефіцієнта Пуассона для повітря?
Як і чому змінюються температура і тиск повітря в балоні під час досвіду?
Який вплив робить на результат запізнювання при закритті крана К1?