1.5.4. Оцінка проникності пласта, що складається з декількох продуктивних прошарків різної проникності
Розглянемо випадок лінійно-горизонтальної фільтрації рідини в пласті, що складається з декількох ізольованих шарів або пропластков пористого середовища (рис. 1.17), розділених між собою нескінченно тонкими непроникними перегородками, різної потужності і проникності.
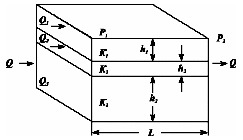
Мал. 1.17. Лінійна фільтрація в пласті, що складається з декількох ізольованих пропластков різної потужності і проникності
Середня величина коефіцієнта проникності пласта буде оцінюватися з урахуванням потужності продуктивних прошарків, через які йде фільтрація флюїдів:
де - середня проникність пласта; ki - проникність i-го пропластками; hi - потужність (висота) i-го пропластками.
Розглянемо приклад. Розрахувати величину середнього коефіцієнта проникності пласта, що складається з декількох ізольованих пропластков для умов:
Дано: № уч-ка hi, м ki, мД
Знайти середній коефіцієнт проникності () пласта?
Рішення. = (100 · 6 + 200 · 4,5 + 300 · 3 + 400 · 1,5) / (6 + 4,5 + 3 + 1,5) = 200 (МД).
При горизонтально-лінійної фільтрації рідини через пласт, що має кілька паралельно послідовно розташованих ізольованих зон пористого середовища різної проникності (рис. 1.18), середня величина коефіцієнта проникності такого пласта розраховується з урахуванням протяжності (довжини) фільтрації флюїдів за рівнянням:
де - середня проникність пласта; ki - проникність i-го пропластками; Li - довжина i-го пропластками; Lобщ = ΣLi - загальна довжина пласта.
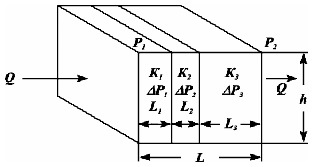
Мал. 1.18. Лінійна фільтрація через пласт, що має кілька послідовно розташованих зон різної проникності
Розглянемо приклад. Розрахувати середній коефіцієнт проникності пласта для горизонтально-лінійної фільтрації рідини, що має кілька паралельно послідовно розташованих ізольованих зон різної проникності з урахуванням умов:
Знайти середній коефіцієнт проникності () пласта?
Рішення. = (75 + 75 + 150 + 300) / (75/25 + 75/50 +150/100 +300 / 200) = 600 / 7,5 = 80 (МД).
При радіальної фільтрації рідини через пласт, що має кілька концентрично розташованих зон різної проникності (рис. 1.19), середня величина коефіцієнта проникності пласта оцінюється з урахуванням радіуса контуру радіальної фільтрації флюїдів через продуктивні пропластки за виразом:
де - середня проникність пласта; ki - проникність зон; ri - радіус i-тій зони; rc - радіус свердловини; rk - радіус контуру харчування.
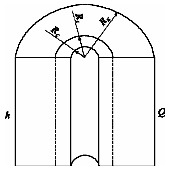
Мал. 1.19 Радіальна фільтрація через пласт, що має кілька концентрично розташованих зон різної проникності
Розглянемо приклад. Розрахувати середній коефіцієнт проникності пласта для випадку радіальної фільтрації рідини з урахуванням умов:
Знайти середній коефіцієнт проникності () пласта?
1.5.5. Залежність проникності від пористості
Теоретично доведено, що для добре відсортованого, обкатаного, однорідного матеріалу (наприклад, кварцовий мономіктовий пісок, представлений на 90% одним мінералом) проникність не залежить від пористості.
Для реальних колекторів в загальному випадку більш пористі породи є і більш проникними.
Залежність проникності від розміру пір для фільтрації через капілярні пори ідеальної пористого середовища можна оцінити з співвідношень законів Пуазейля і Дарсі.
Рівняння Пуазейля описує об'ємну швидкість течії рідини через пористе середовище, яка подається у вигляді системи прямих трубок однакового перетину довжиною (L), що дорівнює довжині пористого середовища:
де r - радіус порового каналу;
L - довжина порового каналу;
n - число пір, що припадають на одиницю площі фільтрації;
F - площа фільтрації;
Р - перепад тиску.
Коефіцієнт пористості середовища, через яку проходить фільтрація, можна представити таким чином:
З урахуванням 1.26, рівняння 1.25 можна переписати таким чином:
і порівняти його з рівнянням Дарсі ().
Прирівнявши праві частини рівнянь, після скорочення подібних членів отримаємо вираз для взаємозв'язку проникності, пористості і радіусу порового каналу:
Вираз 1.28 використовується при проведенні прогнозних і модельних розрахунках коефіцієнта проникності для зразків кернового матеріалу з відомою пористістю. Вимірювання показали, що радіуси пір, за якими в основному відбувається рух рідин, знаходиться в межах від 5 до 30 мкм.
З рівняння 1.28 випливає, що радіус (розмір) порового каналу можна оцінити:
Якщо виразити проникність в мкм 2. то радіус порових каналів (в мкм) буде розраховуватися за виразом:
Рівняння 1.28-1.30 характеризують взаємозв'язок між пористістю, проникністю і радіусом порового каналу і справедливі тільки для ідеальної пористого середовища, наприклад, для кварцового піску.
Для реальних колекторів оцінка радіуса порового каналу проводиться з урахуванням структурних особливостей порового простору порід. Узагальненим вираженням для цих цілей є емпіричне рівняння Ф.І. Котяхова:
де r - радіус пор;
- структурний коефіцієнт, що враховує звивистість порового простору.
Значення оцінюють для модельних середовищ шляхом вимірювання електричного опору порід. Для керамічних, пористих середовищ при зміні пористості від 0,39 до 0,28, за експериментальними даними, змінюється від 1,7 до 2,6. Структурний коефіцієнт для зернистих порід можна приблизно оцінити за емпіричною формулою:
Для оцінки взаємозв'язку коефіцієнта проникності від радіуса порового каналу при фільтрації рідини тільки через канали, капіляри (пори круглого перетину) використовуються співвідношення рівнянь Пуазейля і Дарсі:
Причому, пористе середовище являє собою систему трубок. Загальна площа пір, через які йде фільтрація флюїдів, оцінюється як:
F = р · r 2. Величину р можна уявити як → р = F / r 2. Підставивши цю величину в рівняння Пуазейля (1.33, ліве вираз) і скоротивши однакові параметри в виразах (1.33, лівому і правому) отримаємо кореляційний взаємозв'язок між коефіцієнтом проникності породи від радіуса порового каналу:
Якщо r вимірюється в [см], а коефіцієнт проникності в [Д] (1Д ≈ 1,02 · 10 -8 см 2 або = 1,01327), то вводиться відповідний коефіцієнт перерахунку 9,869 · 10 -9. Тоді, коефіцієнт проникності при фільтрації рідини через капіляр оцінюється емпіричним виразом:
Оцінка взаємозв'язку коефіцієнта проникності від висоти поровой тріщини при фільтрації рідини тільки через тріщинуваті пори оцінюється з співвідношень рівнянь Букінгема і Дарсі.
Втрата тиску при течії рідини через щілину дуже малої висоти оцінюються рівнянням Букінгема:
де h - висота тріщини;
v - лінійна швидкість фільтрації рідини.
Висловивши з рівняння Дарсі величину перепаду тиску (ΔP = v · м · L / kпр.), Прирівнявши праві частини з 1.36 і скоротивши однакові параметри отримаємо вираз:
З урахуванням того, що h вимірюється в [см], а коефіцієнт проникності в [Д], вводиться відповідний коефіцієнт перерахунку = 9,869 · 10 -9. Тоді, коефіцієнт проникності при фільтрації рідини через тріщину оцінюється:
Рівняння 1.35 і 1.38 використовується для теоретичної оцінки коефіцієнтів проникності для конкретного виду пір.
Розглянемо приклад. Через кубик породи розміром 10 х 10 х 10 см, з проникністю 10 МД фільтрується рідина при лінійної режимі в'язкістю 1 СПЗ, при градієнті тиску (? Р / ΔL), що дорівнює 0,25 атм / м (0,0025 атм / см) . Визначити дебіт?
Рішення. Розглянутий випадок - субкапіллярной фільтрації, тобто фільтрація рівномірна і проходить через всю площу зразка, що має субкапіллярную пористість. Дебіт (Q1) складе:
= 100 · 0,01 · (0,0025 / 1) = 0,0025 см 3 / сек.
Якщо в цьому кубику буде один канал діаметром 0,2 мм тієї ж довжини, що і кубик, то при тому ж градієнті тиску дебіт фільтрується рідини через цей канал буде:
= 12,5 · 10 6 · (0,02 / 2) 2 · р · (0,02 / 2) 2 · 0,00025 = 0, 001 см 3 / сек
Отже, при наявності в кубику одного каналу і субкапіллярной пористості, т. Е. При наявності нерівномірної фільтрації сумарний дебіт (Q3) фільтрується рідини складе:
Сумарний дебіт (Q3) має величину на 40% більше ніж при субкапіллярной фільтрації (Q1).
Якщо в кубику замість каналу є тріщина висотою 0,2 мм і шириною 10 см, її вплив на загальний дебіт рідини, що фільтрується через породу, буде істотним:
= (84,4 · 10 5 · (0,02) 2 · 0,02 · 10 · 0,0025) / 1 = 1,688 см 3 / сек.
А сумарний дебіт (Q5) з урахуванням субкапіллярной фільтрації (Q1) складе:
У порівнянні з першим випадком дебіт збільшиться в 675 разів.
Приклад свідчить про великий вплив наявності каналів і особливо тріщин в породі на обсяг фільтрується рідини.
На практиці проникність породи визначають в лабораторних умовах з керновому матеріалу (див. Лабораторний практикум).