
Головна | Про нас | Зворотній зв'язок
Мікросхеми сумматоров (англійське Adder), як випливає з їх назви, призначені для підсумовування двох вхідних двійкових кодів, тобто вихідний код буде дорівнює арифметичній сумі двох вхідних кодів. Наприклад, якщо один вхідний код - 7 (0111), а другий - 5 (0101), то сумарний код на виході буде 12 (1100). Сума двох двійкових чисел з числом розрядів N може мати число розрядів (N + 1). Наприклад, при підсумовуванні чисел 13 (1101) і 6 (0110) виходить число 19 (10011). Тому кількість виходів суматора на одиницю більше кількості розрядів вхідних кодів. Цей додатковий (старший) розряд називається виходом перенесення.
На схемах суматори позначаються буквами SM. У вітчизняних серіях код, що позначає мікросхему суматора, - ІМ.
Суматори бувають однорозрядні (для підсумовування двох однорозрядних чисел), 2-х розрядні (підсумовують 2-х розрядні числа) і 4-х розрядні (підсумовують 4-х розрядні числа). Найчастіше застосовують саме 4-розрядні суматори. На рис. 6.1 показані для прикладу 2-розрядний і 4-розрядний суматори. Мікросхема ІМ6 відрізняється від ІМ3 тільки підвищеною швидкодією і номерами використовуваних висновків мікросхеми, функція ж виконується та ж сама.
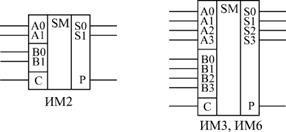
Мал. 6.1. Приклади мікросхем суматорів
Крім вихідних розрядів суми і виходу переносу, суматори мають вхід розширення (інша назва - вхід переносу) С для об'єднання декількох сумматоров з метою збільшення розрядності. Якщо на цей вхід приходить одиниця, то вихідна сума збільшується на одиницю, якщо ж приходить нуль, то вихідна сума не збільшується. Якщо використовується одна мікросхема суматора, то на її вхід розширення С необхідно подати нуль.
Для прикладу в табл. 6.1 приведена повна таблиця істинності 2-розрядної сумматора ІМ2. Як видно з таблиці, вихідний 3-розрядний код (Р, S1, S0) дорівнює сумі вхідних 2-розрядних кодів (А1, А0) і (В1, В0), а також сигналу С. Нульові розряди - молодші, перші розряди - старші . Повна таблиця істинності 4-розрядного суматора буде надмірно великий, тому вона не наводиться. Але суть роботи залишається точно такий же, як і в випадку 2-розрядної суматора.
Суматори можуть використовуватися також для підсумовування чисел в негативній логіці (коли логічній одиниці відповідає електричний нуль, і навпаки, логічному нулю відповідає електрична одиниця). Але в цьому випадку вхідний сигнал перенесення З також стає інверсним, тому при використанні однієї мікросхеми суматора на вхід С треба подати електричну одиницю (високий рівень напруги). Інверсним стає і вихідний сигнал перенесення Р, низький рівень напруги на ньому (електричний нуль) відповідає наявності перенесення. Тобто виходить, що акумулятор абсолютно однаково працює як з позитивною, так і з негативною логікою.
Таблиця 6.1. Таблиця істинності мікросхеми 2-розрядної сумматора ІМ2
Розглянемо приклад. Нехай нам треба скласти два числа 5 і 7 в негативній логіці. Числа 5 в позитивній логіці відповідає двійковий код 0101, а в негативній - код 1010. числа 7 в позитивній логіці відповідає двійковий код 0111, а в негативній - код 1000. При подачі на вхід суматора кодів 1010 (десяткове число 10 в позитивній логіці) і 1000 (десяткове число 8 в позитивній логіці) отримуємо суму 10 + 8 = 18, тобто код 10010 в позитивній логіці. З урахуванням вхідного сигналу переносу С = 1 (відсутність вхідного перенесення в негативній логіці) вихідний код суматора вийде на одиницю більше: 18 + 1 = 19, тобто 10011. При негативній логіці це буде відповідати числу 01100, тобто 12 при відсутності вихідного перенесення . В результаті отримали 5 + 7 = 12.
Суматор може обчислювати не тільки суму, але і різниця вхідних кодів, тобто працювати вичітателя. Для цього від'ємник число треба просто поразрядно проинвертировать, а на вхід перенесення З подати одиничний сигнал (рис. 6.2).
Мал. 6.2. 4-х розрядний вичітатель на сумматоре ІМ6 і инверторах ЛН1
Наприклад, нехай нам треба обчислити різницю між числом 11 (1011) і числом 5 (0101). Інвертуємо поразрядно число 5 і отримуємо 1010, тобто десяткове 10. Суматор при підсумовуванні 11 і 10 дасть 21, тобто двійкове число 10101. Якщо сигнал С дорівнює 1, то результат буде 10110. відкидаємо старший розряд (вихідний сигнал Р) і отримуємо різницю 0110, тобто 6.
Ще приклад. Нехай треба обчислити різницю між числом 12 (1100) і числом 9 (1001). Інвертуємо поразрядно 9, отримуємо 0110, тобто десяткове 6. Знаходимо суму 12 і 6, отримуємо 18, а з урахуванням С = 1 отримуємо 19, тобто двійкове 10011. У чотирьох молодших розрядах маємо 0011, тобто десяткове 3.
Каскадувати суматори для збільшення розрядності дуже просто. Треба сигнал з виходу перенесення суматора, який займається обробкою молодші розряди, подати на вхід перенесення суматора, який займається обробкою старші розряди (рис. 6.3). При об'єднанні трьох 4-розрядних суматорів виходить 12-розрядний суматор, який має додатковий 13-й розряд (вихід перенесення Р).
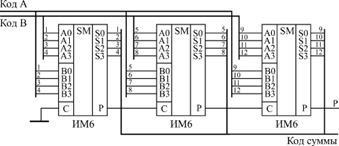
Мал. 6.3. Каскадування сумматоров ІМ6 для збільшення розрядності
Невизначені стану на виходах суматора можуть виникати при будь-якій зміні будь-якого з вхідних кодів (рис. 6.4). Вихідний код суми може приймати протягом короткого часу значення, ніяк не пов'язані з вхідними кодами, а на виході перенесення можуть з'являтися короткі паразитні імпульси. Це пов'язано перш за все з неодночасним зміною розрядів вхідних кодів. Щоб уникнути впливу цих невизначених станів на подальшу схему, необхідно передбачати синхронізацію або стробирование вихідних сигналів. Але для цього треба мати інформацію про моментах зміни вхідних кодів, яка є далеко не завжди.
Мал. 6.4. Невизначені стану на виходах суматора при зміні вхідних кодів
Затримки сумматора ІМ6 від входів до виходів суми приблизно вдвічі перевищує затримку логічного елемента, а від входів до виходу переносу - приблизно в півтора рази. Затримки сумматора ІМ3 більше затримок ІМ6 майже вдвічі. Тому в схемах, де важливо швидкодію, краще використовувати ІМ6. Особливо це істотно при каскадування для збільшення розрядності, так як там затримки окремих мікросхем підсумовуються. Точні величини затримок треба дивитися в довідниках.
Арифметичне-логічний пристрій - схема комбінаційного типу, що не вимагає для своєї роботи будь-яких прив'язаних до часу тактових сигналів. Результат операції з'являється на виході АЛУ через затримку, що дорівнює сумі затримок логічних елементів, що утворюють найдовшу ланцюг всередині АЛУ. Через послідовного проходження перенесення через все розряди АЛУ, довжина найдовшої ланцюга, а отже, і загальна затримка АЛУ зростає пропорційно його розрядності. Грубо кажучи, затримка 32-розрядної АЛУ буде в 32 рази більше, ніж затримка однорозрядного АЛУ. Використання спеціальних схем прискореного перенесення дозволяє в кілька разів зменшити затримку багаторозрядних АЛП.
У загальному випадку багатофункціональне АЛУ включає операційну частину (ОУ) і пристрій керування (УУ), яке здійснює вторинну дешифрацию коду команди і визначає виконувану в АЛУ операцію.
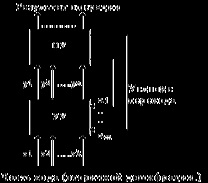
Малюнок 4.2. структура АЛУ
Набір виконуваних в АЛУ операцій повинен володіти функціональної повнотою. Щоб забезпечити функціональну повноту досить чотирьох операцій:
- звернення до пам'яті для запису / читання даних;
- інкремент / декремент;
- порівняння (реалізує можливість умовного переходу);
- зупинка роботи пристрою.
У перших процесорах кількість операцій обмежувалося шістнадцятьма, тепер досягає декількох сотень.
Кількість виконуваних операцій є важливою характеристикою АЛУ.
АЛУ можна класифікувати за рядом ознак, наведених нижче.
Класифікація за способом подання даних:
- з фіксованою комою;
- з плаваючою комою.
2. Класифікація за способом дії над операндами:
· Послідовні АЛУ, де кожна операція виконується послідовно над кожним розрядом;
· Паралельні АЛУ, операція виконується над усіма розрядами даних одночасно;
· Послідовно - паралельні АЛУ, де слово даних ділиться на склади, обробка даних ведеться паралельно над розрядами складу і послідовно над складами.
3. Класифікація за використання систем числення:
4. Класифікація за характером використання елементів і вузлів:
- блочние- для виконання окремих арифметичних операцій в структуру АЛУ вводять спеціальні блоки, що дозволяє процес обробки інформації вести паралельно;
- конвейерние- в конвеєрних АЛУ операція розбивається на послідовність мікрооперацій, виконуваних за однакові проміжки часу (такти) на різних щаблях конвеєра, що дозволяє виконувати операцію над потоком операндів кожен такт;
- многофункціональние- це універсальні АЛП, що виконують безліч операцій в одному пристрої. У таких АЛУ потрібно налаштування на виконання даної операції за допомогою коду операції.
5.Класифікація по тимчасовим характеристикам.
За часовими характеристиками АЛУ діляться на:
- сінхронние- в синхронних АЛУ кожна операція виконується за один такт.
- асінхронние- НЕ тактовані АЛУ, що забезпечують високу швидкодію, так як виконуються на комбінаційних схемах.
6.Классіфікація по структурі пристрою управління: