Бібліографічний опис:
1. Введення Побудова системи, що забезпечує необхідну якість при впливі на об'єкт зовнішніх збурень, є однією з основних проблем сучасної теорії управління. У класі задач робастного управління існує велика кількість методів і підходів до вирішення даного завдання. Найбільш повно робастний теорія і бібліографія по ній представлена в [1]. Алгоритм управління, побудований з використанням внутрішньої моделі гармонійних коливань, отриманий в [2-5]. Але однією з основних проблем при синтезі систем управління, що дозволяють компенсувати обурення, є завдання формування сигналу, що несе інформацію про них, і що дозволяє використовувати його для отримання потрібних оцінок. І ця проблема вирішена в [6-9], де використовується метод допоміжного контуру, який дозволяє виділити сигнал, що несе інформацію про перешкоди, отримати необхідні оцінки і компенсувати небажаний вплив перешкод на регульовані параметри. У даній роботі запропоновано спосіб побудови системи управління для лінійного об'єкта, у якого всі параметри відомі, а на вході і на регульованому виході діють обурення, причому обурення ці різні, причому для цього не потрібно ніяких апріорних знань про параметри зовнішніх збурень. Спроектована система управління дозволяє компенсувати вплив перешкод на регульовані змінні із заданою точністю і зробити їх незалежними від що не вимірюваних необмежених збурень на вході системи. Основні результати отримані з використанням технології конструктивного вкладення систем [10] і методу допоміжного контуру [6-9].
Об'єкт управління заданий у вигляді рівнянь (1) - (3):
(3) де. . . - вектори стану, управління, вимірюваних і регульованих параметрів відповідно, - вектор зовнішніх збурень, - шум на виході статичного ланки моделі системи; - початкові умови; - числові матриці відповідних порядків. Потрібно забрати алгоритм функціонування системи управління, яка забезпечує виконання цільового умови (4) при. де - досить мала величина, - час, після закінчення якого повинна забезпечуватися необхідна динамічна точність після включення системи в роботу.
пара - керована, а пара - наблюдаема;
обурення на вході системи - обмежена функція;
i ii) перешкода на виході системи - обмежена функція;
i v) все матриці в (1) - (3) відомі.
Інші обмеження будуть приведені в умовах утвердження.
Будемо формувати вектор управління у вигляді
(5). де - допоміжний управління вимірюванням; - числова матриця регулятора.
Попередні відомості про канонізацію матриць
Якщо матриця неповна (необоротна), вона містить лінійно залежні рядки і / або стовпці. Для опису лінійної залежності і незалежності рядків і стовпців матриці зручно використовувати поняття дільників нуля максимального рангу і канонізаторов. В [10] канонізацією названо не обов'язково єдине розкладання будь-якої матриці розміру і рангу на четвірку матриць, що задовольняють наступним рівності в блокової записи де і - лівий і правий подільники нуля максимального рангу, і - лівий і правий канонізатори (. - одинична матриця розміру). Для будь-якої матриці лівий (правий) дільник нуля максимального рангу характеризує всі лінійно залежні комбінації рядків (стовпців) вихідної матриці відповідно до тотожністю (). При вирішенні матричних рівнянь методом канонізації використовується поняття зведеного канонізатора. обчислюється за формулою і задовольняє умовам регулярності по Нейману. . Зведений канонізатор характеризує сукупність лінійно незалежних комбінацій рядків і стовпців початкової матриці. Окремим випадком зведеного канонізатора є псевдообернена матриця по Муру - Пенроуза. Для матриці повного строчечного рангу зведений канонізатор збігається з правим дільником одиниці. а для матриці повного столбцовую рангу - з лівим дільником одиниці. Правим (лівим) делителем одиниці для матриці розміру повного строчечного (столбцовую) рангу називається матриця (), яка задовольнить умові (). Для визначення параметрів регулятора, скористаємося твердженням, сформульованим В.Н. Буковим [10, с.473]. Затвердження 1.Система (1) - (3) при заданих матрицях володіє инвариантностью до збурень в сенсі тождестватогда і тільки тоді, коли виконуються наступні умови: 1) існує ненульова калібрувальна матриця інваріантності. для якої виконується умова,; 2) матриця ефективності обурення належить множині, де - довільна числова матриця відповідного розміру; 3) система, замкнута будь-яким регулятором (6) з безлічі (6), де - матриці відповідних розмірів з довільними елементами [10].
-
синтез управління
Використовуємо закон управління (5), тоді рівняння об'єкта (1) - (3) набуде вигляду. де матриця Гурвіцева, тобто власні числа задовольняють умові. За допомогою технології конструктивного вкладення систем, визначивши регулятор за формулою (6), ми добиваємося того, що передавальна функція від обурення до регульованого виходу стане дорівнює нулю, і, відповідно, компонента компенсується. Далі перейдемо до подання системи у вигляді вхід - вихід, (7) де - оператор диференціювання; . - транспонована матриця алгебраїчних доповнень матриці; . . Далі скористаємося методом допоміжного контуру, і виділимо сигнал, що несе інформацію про перешкоди, для чого візьмемо підсистему, яка описується рівнянням (8). і складемо рівняння для сигналу неузгодженості. віднімаючи (8) з (7): (9). З рівняння (9) виділимо сигнал (10). Для реалізації (10) потрібно гурвіцевость полінома. що можна забезпечити відповідним підбором матриці. Однак такий підбір не завжди можливий. Таким чином, повинна існувати матриця. забезпечує гурвіцевость полиному. що є додатковим обмеженням, що не вказані у припущенні. Оскільки. то (9) піддається реалізації, і сформувавши допоміжний сигнал управління в вигляді (11) отримаємо рівняння для вектора стану об'єкта. Затвердження 2.Пусть виконані умови припущень і існує матриця. забезпечує стійкість чисельника передавальної функції (8). Тоді керуючий пристрій, динамічні процеси в якому описуються рівняннями (5), (6), (8), (11) забезпечує виконання цільового умови (4).
-
приклад
Розглянемо задачу стабілізації для об'єкта управління, динамічні процеси в якому описуються рівняннями (1) - (3). . . . . . Формуємо закон управління в вигляді. Умови затвердження 1 виконуються. Для спрощення приймемо всі варійовані параметри рівними нулю і отримаємо наступну матрицю регулятора Допоміжне керуючий вплив формуємо у вигляді. де. . Для розглянутого прикладу отримаємо наступне допоміжне керуючий вплив. Тоді отримаємо матрицю у допоміжному контурі
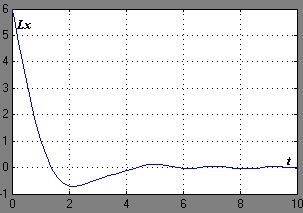
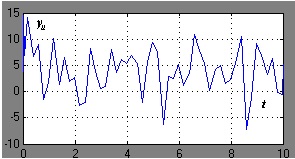
. з власними числами. На рис. 1 наведені результати моделювання системи управління при наступних вихідних даних: початкові умови. впливи на вході і. шум на виході являє собою випадковий сигнал.
Мал. 1. Перехідні процеси в системі, коли випадковий сигнал В даному випадку цільове умова виконується через 8 секунд.
Розв'язана задача побудови робастної системи керування лінійним стаціонарним об'єктом без запізнень і будь-яких обмежень на управління, яка дозволила компенсувати обурення на вході і на виході системи, причому обурення ці різні. Спроектована система управління дозволяє компенсувати вплив збурення на регульовані змінні із заданою точністю, що продемонстровано на прикладі.
Основні терміни (генеруються автоматично). системи управління, Алгоритм робастного управління, зовнішніх збурень, управління лінійним, нуля максимального рангу, робастного управління лінійним, Цикунов А.М, Спостерігачі зовнішніх збурень, Спроектована система управління, лінійним об'єктом, Компенсація збурень, матриці розміру, допоміжного контуру, вихідної матриці, управління лінійним об'єктом, матриця ефективності обурення, системи управління лінійним, матриці повного, закон управління, управлінні лінійним об'єктом.