- кінцеве безліч точок, прямих, площин, пов'язаних між собою взаємними Інцидентне. К. можуть бути як плоскими, так н просторовими.
Плоска конфігурація - кінцева система рточек і gпрямих на площині, розташованих таким чином, що будь-яка точка системи инцидентна з одним і тим же числом упертих цієї системи, а будь-яка пряма инцидентна з одним і тому ж числом p точок цієї системи. Мінімальна система точок даної К. з до-рій вся К. може бути отримана шляхом інціденцій пар точок з прямими і перетинів пар прямих, наз. системою утворюючих даної К. Числа р, g, g, p пов'язані співвідношенням pg = g p, a К. позначається символом (р g, gp). К. містить однакове число точок і прямих, позначається символом (р у).
Приклади плоских К. 1) Одна точка і одна пряма, інцідентние між собою, утворюють К. (11). 2) Три точки, що не лежать на одній прямій, і три прямі, інцідентние з кожною парою, утворюють К. (32),
ця фігура - трехвершинников (або трехстороннік) на площині. 3) Повний четирехсторонников - чотири прямі і шість точок їх попарного перетину утворюють К. (62. 43). Однак тут не все прямі, що з'єднують попарно точки К. є прямими цієї К .; точки R, P, Q і прямі RP, RQ, PQ не належать їй (рис. 1).
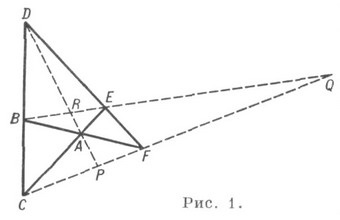
Автоморфізмом К. зв. відображення К. на себе, при к-ром точки К. переходять в точки, прямі - в прямі цієї ж К. і при цьому жодна инцидентность не пропадає, і не додається нових. К. зв. правильною, якщо група автоморфізмів цієї К. транзитивна.
Для даної К. (р g, gp) двоїстої зв. К. (gp. Р g). К. типу (р g) н тільки такі, двояко відповідають К. такого ж типу, вони зв. двояко-інваріантними.
К. зв. проективної, якщо инцидентность її елементів зберігається при проектних перетвореннях. Напр. инцидентность елементів деякої К. розташованої на проективної площині, забезпечується виконанням аксіом зв'язку її, і тому инцидентность точок і прямих К. зберігається при проектних перетвореннях цій площині, а К. буде проективної. Все инцидентности і елементи такої плоскої К. можуть бути зображені на кресленні за допомогою тільки однієї лінійки. Плоска К. завжди має двоїсту внаслідок принципу подвійності.
К. може бути визначена також як кінцева часткова площину. Можливість існування деякої К. визначається з геометрпч. н комбінаторних співвідношень між кількістю точок і прямих і кількістю взаємних інціденцій. К. задається і за допомогою абстрактних схем, напр, на таблиці (рис. 2) вказані инцидентности (позначені хрестиком) чотирьох точок, вершин А i, і чотирьох площин, граней Di тетраедра. Після того як недо-раю К. визначена абстрактно, виникає питання про її реалізації, т. Е. Про можливість побудови всіх інціденцій по даній системі утворюють. Реалізація К. як кінцевої часткової площині означає можливість изоморфного відображення її на недо-рую подплоскость будь-якої площини.
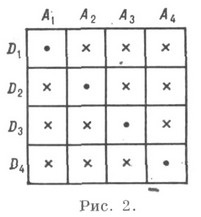
К. (р 2), реалізується у вигляді р-прихильника так, що вершини і сторони його попарно інцидентні. Абстрактну схему К. (32) можна побудувати, напр. таблицею, як на рис. 2. Плоскі К. (р 3) можливі лише при тому що через кожну точку К. повинні проходити три прямі і на кожній з них повинні лежати ще дві інші точки К. (число р має задовольняти нерівності). К. типу (р 3) допускають модифікації, кількість яких брало залежить від р. К. (73) представляється схемою (рис. 3),
де цифра за фігурною дужкою означає точку перетину прямих, що проходять через пари точок, записані зліва від дужки, цифри за вертикальною лінією позначають, ті точки, к-які повинні бути колінеарними при виконанні всіх зазначених зліва інціденцій. На дійсній проектній плоскості все инцидентности реалізуються в повному четирехвершінніке (рис. 4),
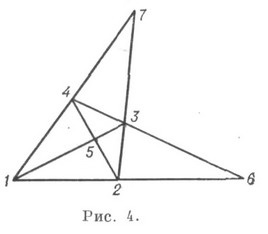
проте остання інціденцій (коллинеарность трьох точок) тут не має місця. К. (93) допускає три різні модифікації, одна з яких брало (93) 1 зв. конфігурацією Бріаншона - Паскаля (рис. 5): кожна пряма li инцидентна з трьома різними точками а, -, а кожна точка - з трьома різними прямими.
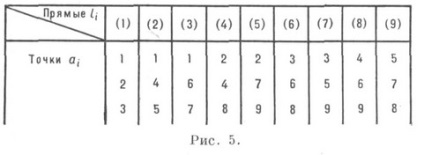
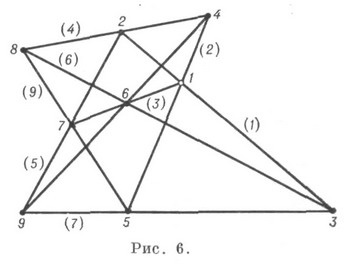
Ця К. може бути реалізована на проективної плоскоcті (рис. 6), вона є проективної, правильної, двояко інваріантної (див. Бріаншона теорема. Паскаля теорема).
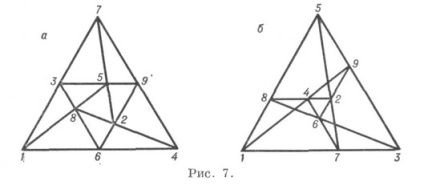
Дві інші модифікації К. (93) 2. (93) 3 (рис 7) істотно відрізняються від конфігурації Бріаншона -Паскаля. Напр. К. (93) 3 не є правильною, а для побудови К. (93) 2 необхідна вспомогательнаякрівая 2-го порядку.
К. (103) має вже десять різних модифікацій, з яких брало найважливішою є конфігурація Дезарга (рис. 8).
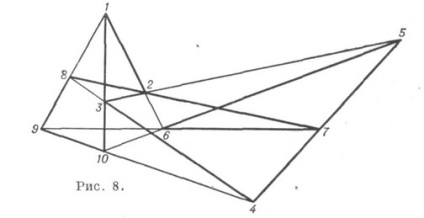
Вона реалізується на дійсній проектній плоскості, є проективної, правильної, двояко інваріантної. Інші дев'ять модифікацій. (103) не виражають ніякої загальної геометричний. теореми, причому лише вісім з них можуть бути реалізовані на дійсній проектній плоскості, але для їх побудови потрібне спеціальне розташування системи утворюють точок (зокрема, К. такого типу реалізуються у вигляді правильних многосторонніков (рис. 9).
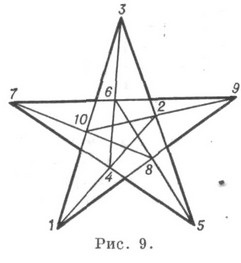
У наведеній на кресленні послідовності вершин також виходить вписаний і одночасно описаний десятістороннік. К. (93) і (103) також допускають геометричний. побудова за допомогою многосторонніков, вписаних і описаних навколо самих себе, так, К. (93) 1 представляється у вигляді девятісторонніка (2, 3, 6, 1, 5, 9, 4, 8, 7, 2) (рис. 6) , конфігурація Дезарга - у вигляді десятісторонніка (рис. 8) (1, 2,3,4,5,6, 7, 8,9, 10, 1). Такі уявлення цих К. єдині точністю до автоморфізмів. Взагалі, побудова р-прихильників, одночасно вписаних й описаних навколо самих себе, призводить до К. типу (р 3). Існують також уявлення К. типу (р 3) у вигляді декількох многосторонніков, вписаних і описаних навколо один одного.
Напр. конфігурація Дезарга допускає єдиний спосіб (з точністю до автоморфізм) уявлення парою взаємно вписаних і описаних пятісторонніков (1, 9, 7, 5, 3) і (8, 4, 10, 6, 2) (рис. 8). При збільшенні числа рколічество модифікацій К. типу (р 3). швидко зростає.
Просторова конфігурація - кінцева система точок і площин така, що кожна точка инцидентна з одним і тим же числом площин, а кожна площина - з одним і тим же числом точок. Поряд з К. складається з точок і площин, в просторі розглядаються і К. складаються з точок і прямих. Так, розглянута вище конфігурація Дезарга, що складається з точок і прямих, предедавляет собою також і просторову К. (103) (рис. 8), якщо відповідні трехстороннікі лежать в різних площинах; одночасно її можна розглядати як К. (103. 56), складену з точок і площин: шість вершин відповідних трехсторонніков, центр перспективи і три точки на осі перспективи, в яких брало сходяться відповідні сторони трехсторонніков, дають всього десять точок, а три площини , утворені відповідними сторонами трехсторонніков, і дві площини самих трехсторонніков дають всього п'ять площин. У кожній площині шість точок К. і кожна точка инцидентна трьом різним площинах.
Тривіальної просторової К. типу (р g). є К. (43), її схема - на рис. 2; вона зображується тетраедром. К. типу (р 4) для неможлива, при р = 8 є п'ять різних схем К. одна з яких брало, так зв. конфігурація Мебіуса, складається з двох тетраедрів, вписаних і описаних один біля одного. Кожній з восьми точок - вершин тетраедрів - інцидентні чотири площині граней тетраедрів, а кожної з восьми площин інцідентни чотири точки - вершини. При переході до К. вищого порядку число можливих модифікацій швидко зростає, напр. К. (94) має вже 26 геометричний. здійсненних модифікацій.
З просторових К. вищого порядку примітні конфігурація Рейє і конфігурація Шлефлі. Конфігурацією Рейє зв. що складається з точок і площин К. (126). У дійсному проектному просторі її можна побудувати, напр. з вершин деякого куба, його центру, трьох (нескінченно віддалених) точок, в яких брало сходяться паралельні ребра куба, а площинами цієї К. є шість граней куба і шість його діагональних площин, що проходять через пари протилежних ребер (рис. 10 ).
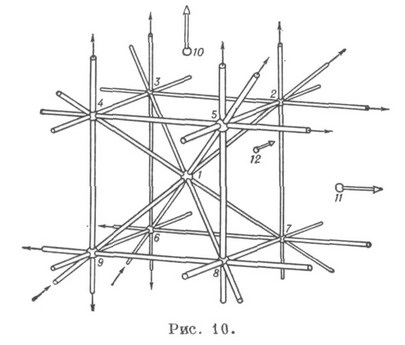
Конфігурація Рейє є проективної, правильною і двояко інваріантної, причому зображення цієї К. можна побудувати (згідно великим принципом подвійності), використовуючи замість куба октаедр (рис. 11).
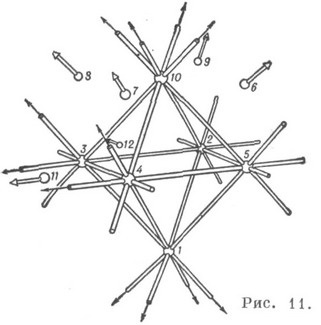
Конфігурацію Рейє можна розглядати також як просторову К. точок і прямих (124. 163). К. (302. 125), що складається з точок і прямих, наз. подвійним шестісторонніком Шлефлі. Він зображується в просторі, напр. у вигляді симетрично розташованих прямих і точок на кожній грані куба (по одній з двох шісток) (рис. 12).
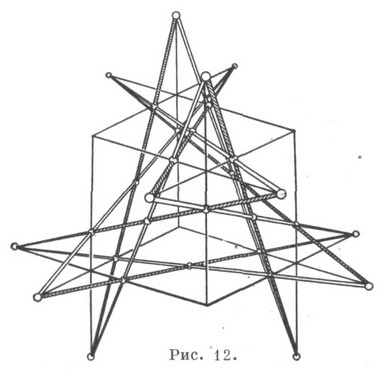
Не всяка плоска К. може бути реалізована на дійсній проектній плоскості. Напр. К. (73) і (83) не реалізуються на ній, в зв'язку з чим виникає задача реалізації К. на будь-яких інших проективних площинах. Кожна пропозиція. яке стверджує, що з реалізованим в даній площині деякої К. з усіма Інцидентне, крім, можливо, однієї, випливає реалізація К. з усіма її Інцидентне, називається конфігураційним пропозицією даної площини. Таким чином, якщо все инцидентности деякої К. реалізуються на даній площині внаслідок геометричних властивостей цієї площини, то К. реалізується на цій площині. Наприклад, К. (93) 1. завжди реалізується на дійсній проектній плоскості, так як з реалізованим всіх інціденцпй, крім однієї, остання инцидентность виконується завжди внаслідок теорем Бріаншона і Паскаля, т. е. ці теореми є конфігураційними пропозиціями. Виконання останньої инцидентности в К. (73) (рис. 4) на такій площині не має місця (так як діагональні точки повного четирехвершінніка не належать одній прямій), тому таке твердження не є конфігураційним пропозицією. Однак воно буде таким в комплексній проективної площині. Подібним чином розглядається і можливість реалізувати інших К .; зокрема, К. (83) може бути реалізована в кінцевих паппових площинах, побудованих над полями Галуа з трьома і чотирма елементами.
Конфігураційні пропозиції, справедливі в цій площині, певним чином організують елементи цієї площини і тому грають роль при аксіоматичному побудові геометрії цій площині. Напр. якщо в даній площині виконуються все аксіоми зв'язку проективної площині, але але реалізується конфігурація Дезарга, то дана площину несе на собі так зв. недезаргову геометрію. Конфігураційне пропозиція може бути також записано в алгебраїч. формі у вигляді деякого алгебраїч. тотожності. У довільній проективної площині конфігураційні пропозиції можуть вводитися лише в якості нових аксіом, причому постулирование одного якогось конфігураційного пропозиції може спричинити за собою справедливість інших конфігураційних пропозицій в цій площині. Взагалі кажучи, кожному алгебраїч. тотожності відповідає конфигурационное пропозицію, до-рої зв. геометричний. поданням цієї тотожності в певній площині, де реалізується К. (проте не встановлено, всяке чи конфигурационное пропозицію є геометричний. поданням певного виду тотожності в алгебрі Тернар і натуральних тел проективної площині). Дослідження подібних алгебраїч. еквівалентів дозволяє вивчати як властивості К. так і можливість їх реалізації як кінцевої часткової площині в певній проективної площині, а також логічний зв'язок між різними конфігураційними пропозиціями.
Теорія К. знаходить застосування у вирішенні ряду геометричних. питань. Так, плоска К. (83) грає важливу роль в теорії плоских кривих третього порядку, що не мають подвійних точок, зокрема, при дослідженні їх точок перегину. Конфігурація Рейє застосовується при вивченні правильних багатогранників в чотиривимірному евклідовому просторі Е 4. Правильний багатогранник в Е 4 обмежений областями, які є правильними тривимірними многогранниками. Правильний багатогранник в Е 4 зв. n-осередком, якщо він обмежений пправільнимі многогранниками. Напр. 5-осередок обмежена п'ятьма тривимірними тетраедрами, 8-осередок - вісьмома кубами і т. Д. Причому 5-осередок і 24-осередок є подвійними самі собі (точки відповідають просторам, а прямі - площинах). Вивчення правильних осередків проводиться дослідженням їх проекцій в Е 3. Якщо в якості простору проекції вибирається для 24-осередки недо-раю трехмернаягрань, то виходить поділ простору на 12-октаедрів, з яких брало все, не рахуючи середнього, простягаються в нескінченність. що призводить до такого виду проекції, к-раю становить конфігурацію Рейє (рис. 10). Якщо в якості простору проекції береться тривимірний простір. що проходить через вершину 24-осередки, то виходить також конфігурація Peйe (рис. 11). (Проекція 24-осередки в тривимірний простір - на рис. 13.)
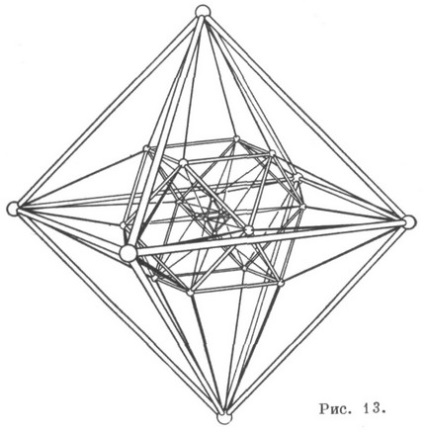
Конфігурація Рейє виникає і в системі точок і осей подібності чотирьох куль, центри яких брало чи не лежать все в одній площині. У цій системі кожна вісь инцидентна з трьома крапками, і кожна точка - з чотирма осями, виходить просторова К. (124. 163) точок і прямих. Кожні три точки - центри подібності - визначають по одній площині, кожні дві осі, інцідентние з точкою подібності, утворюють ще вісім різних площин, всього 12, кожна з яких брало инцидентна з шістьма точками подібності, а кожна з дванадцяти точок подібності - з шістьма площинами, т. е. виходить К. (126). К. надається подвійним шестісторойніком Шлефлі, застосовується для вивчення властивостей алгебраїч. поверхонь третього порядку, до-раю визначається 19 точками і завжди проходить через недо-рий подвійний шестістороннік Шлефлі. При цьому суттєвим є те, що будь-які чотири прямі його мають гіперболоідальное розташування.
Конфігураційні пропозиції про реалізацію Інцидентне на площині застосовуються для вивчення властивостей многосторойніков (многовершінніков) і для вирішення завдань на побудову при різних обмеженнях (побудова з недоступними елементами, побудова однієї лінійкою і т. Д.). У кінематиці і графічної статиці знаходить практичне застосування теорія К. поліедров.
Можливі К. складені з інших геометричних. елементів, напр, з кіл довільної розмірності і одиничного радіуса в Е п.
Літ. : [1] Гільберт Д. Кой-Фоссен С, Наочна геометрія. пер. з нім. 2 изд. М.-Л. 1951; [2] Скорняков Л. А. "Успіхи матем. Наук", 1951, т. 6, ст. 6, с. 112- 154; [3] Аргунов Б. І. "Матем. Зб.", 1950, т. 26, № 3, с. 425-56; [4] Levi F. Geometrische Konfigurationenen, Lpz. 1929.
Математична енциклопедія. - М. Радянська енциклопедія. І. М. Виноградов. 1977-1985.