Конічний перетин. або коника [1]. - перетин площині з круговим конусом. Існує три основних типи конічних перетинів: еліпс. парабола і гіпербола. крім того, існують вироджені перетину: точка. пряма і пара прямих. Окружність можна розглядати як окремий випадок еліпса.
Конічні перетину можуть бути отримані як перетин площині з двостороннім конусом
Якщо площина проходить через початок координат. то виходить вироджений розтин. У невиродженому випадку,
- якщо січна площина перетинає всі твірні конуса в точках одного його порожнини, отримуємо еліпс,
- якщо січна площина паралельна одній з дотичних площин конуса, отримуємо параболу,
- якщо січна площина перетинає обидві порожнини конуса, отримуємо гіперболу.
Рівняння кругового конуса квадратично, стало бути, все конічні перетину є квадрік. також всі квадрік площині є конічними перетинами (хоча дві паралельні прямі утворюють вироджену квадрік, яка не може бути отримана як перетин конуса, але все ж зазвичай вважається «виродженим конічним перетином»).
Конічні перетину були відомі ще математикам Древньої Греції.
Найбільш повним твором, присвяченим цим кривим, були «Конічні перетини» Аполонія Пергського (близько 200 р. До н.е..). Мабуть він першим описав фокуси еліпса і гіперболи [2]: 41.
Папп Олександрійський першим описав фокус параболи і вивів загальне рівняння для конічного перетину як геометричне місце точок. для яких відношення відстаней до точки фокуса і директриси постійно [2]: 48.
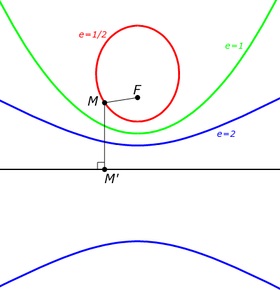
Еліпс (e = 1/2). парабола (e = 1) і гіпербола (e = 2) з фіксованими фокусом F і директоркою.
Все невироджені конічні перетину, крім кола. можна описати в такий спосіб:
Виберемо на площині точку F і пряму d і задамо дійсне число e ≥ 0. Тоді геометричне місце точок. для яких відстань до точки F і до прямої d відрізняється в e раз, є конічним перетином. Точка F називається фокусом конічного перетину, пряма d - директоркою. число e - ексцентриситетом.
Залежно від ексцентриситету, вийде:
Ексцентриситет пов'язаний з параметрами конуса і розташуванням січної площини відносно осі конуса таким співвідношенням [3]: 46,47:
тут ψ - кут нахилу січної площини до осі конуса, φ - кут між твірною і віссю конуса, що дорівнює половині кута розчину конуса. З цієї формули видно, що, перетинаючи даний конус площиною, можна отримати еліпс з будь-яким ексцентриситетом, параболу, а гіперболу можна отримати лише таку, ексцентриситет якої не перевищує 1 cos φ >>. Це максимальне значення досягається при перетині даного конуса площиною, паралельною його осі.
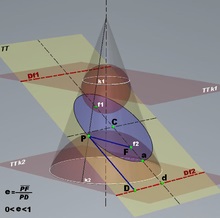
Еліпс (синій) як конічний перетин, що розділяє кулі данделена; директриси еліпса (Df1 і Df2), його фокуси (f1 і f2) і ексцентриситет (e)
Деякі важливі властивості конічних перетинів виходять при розгляді двох куль, що стосуються конічного перетину і конуса - куль Данделі. Наприклад, з їх допомогою встановлюється геометричний сенс фокуса, директриси і ексцентриситету конічного перетину [3]: 46,47.
- Через будь-які п'ять точок на площині, ніякі три з яких не лежать на одній прямій, можна провести єдине конічний перетин.
- Ексцентриситет двох невироджених конічних перетинів збігається тоді і тільки тоді, коли вони можуть бути переведені один в одного перетворенням подібності.
- Афінний перетворення зберігають тільки знак ексцентриситету, тобто з точки зору афінної геометрії існує тільки три різних невироджених конічних перетину: еліпс, парабола і гіпербола.
- Все невироджені конічні перетину невиразні в проективної геометрії.
декартові координати
A x 2 + B x y + C y 2 + D x + E y + F = 0. + Bxy + Cy ^ + Dx + Ey + F = 0,>
визначає тип конічного перетину.
- Якщо дискримінант менше нуля, то це еліпс. точка або порожня множина.
- Якщо дискримінант дорівнює нулю, то це парабола. пряма або пара паралельних прямих.
- Якщо дискримінант більше нуля, то це гіпербола або пара пересічних прямих
полярні координати
У полярних координатах (ρ. Θ). з центром в одному з фокусів і нульовим напрямком уздовж головної осі, конічний перетин представляється рівнянням
де е позначає ексцентриситет і l постійна.
В рамках класичної механіки траєкторія вільного руху сферичних об'єктів в безповітряному просторі підпорядковується одному з додатків закону зворотних квадратів - закону всесвітнього тяжіння. і внаслідок цього є однією з конічних кривих - параболою, гіперболою, еліпсом або прямий. Орбіти планет - еліпси, траєкторії комет - еліпси, гіперболи [4] або «майже параболічні» [5] (див. Також Небесна механіка), траєкторія польоту гарматного ядра без врахування впливу повітря - дуга еліпса (див. Також Балістика).