§1. Електричні заряди і електричне поле. Закон Кулона.
Напруженість електричного поля. принцип суперпозиції
Електричний заряд і електричне поле це фундаментальні поняття, яким неможливо дати строгі визначення через будь-які інші, більш прості поняття. Можна тільки описувати їх властивості.
З досвіду відомо, що електричні заряди бувають двох типів, які умовно названі позитивними і негативними. Тіла, що мають заряди одного знака, відштовхуються один від одного, а різнойменно заряджені тіла притягуються. Заряд будь-якого об'єкта визначається сумарним зарядом елементарних частинок, з яких цей об'єкт складається. Зарядити макроскопическое тіло можна, тільки змінивши число містяться в ньому заряджених елементарних частинок. Електричний заряд дискретний. Абсолютна величина заряду всіх заряджених елементарних частинок однакова і дорівнює елементарному зарядуе = 1,6010 19 Кл. Елементарний заряд дуже малий, так що величину макроскопічних зарядів, як правило, можна вважати мінливої безперервно. Позитивний заряд мають протони, негативний - електрони. Електричний заряд не залежить від стану руху частинки, її взаємодії з іншими об'єктами, і не змінюється при переході від однієї системи відліку до іншої.
В результаті узагальнення дослідних даних був установленфундаментальний закон природи - закон збереження електричного заряду. алгебраїчна сума електричних зарядів будь ізолірованнойсістеми зберігається, які б процеси не відбувалися всередині цієї системи. У сістемемогут утворюватися або зникати електрично заряджені частинки, однак при цьому одночасно народжуються або зникають частки, заряди яких протилежні за знаком і в сумі дорівнюють нулю.
У багатьох задачах електродинаміки користуються моделлю точкового електричного заряду. Точковий електричний заряд- це заряджене тіло, розмірами і формою якого в рассматріваемойзадачеможно знехтувати. Наприклад, при розгляді електростатичного взаємодії двох заряджених тіл, їх можна вважати точковими зарядами, якщо розміри цих тіл багато менше відстані між ними.
Закон взаємодії нерухомих точкових електричних зарядів експериментально встановлений в 1785 р французьким фізиком Ш. Кулоном. Тому сили електростатичного взаємодії часто називають кулоновскими силами.
Закон Кулона формулюється так: сила взаємодії між двома нерухомими точковими зарядами, що знаходяться в вакуумі, пропорційна добутку модулів цих зарядів, обернено пропорційна квадрату відстані між ними і спрямована уздовж з'єднує їх прямий.
На підставі закону Кулона модуль F сили взаємодії точкових зарядовq1 іq2. знаходяться на расстоянііr12 один від одного, записується у вигляді
де k -коеффіціентпропорціональності, що залежить від вибору системи одиниць.
Вектор сили F2. діючої на зарядq2 з боку зарядаq1. можна представити у вигляді:
Відповідно, сила F1. діюча на зарядq1 з боку зарядаq2. дорівнює
Так як r21 = r12. з формул (1.2) і (1.3) следуетF1 = F2. тобто кулонівських сили підпорядковуються третім законом Ньютона.
В системі СІ коефіцієнт пропорційності k в законі Кулона прийнято записувати у вигляді:
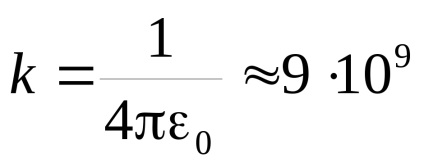
Одиниця заряду кулон (Кл) в системі СІ є похідною. Вона виражається через основну одиницю - ампер (А). Один кулон дорівнює заряду, що протікає через поперечний переріз провідника за одну секунду при силі струму один ампер (1 Кл = 1 А 1 с).
Поряд з системою СІ у фізиці, особливо в теоретичній фізиці, використовується система СГС (гауссова система). Гауссова система з фізичної точки зору є значно більш природною, ніж СІ. Надалі ми зможемо в цьому неодноразово переконатися. Перевага СІ чисто інженерне, тому що при розрахунках чисельні результати відразу виходять в звичних для електротехніки одиницях - амперах, вольтах, Омасі і т.д.
В системі СГС основними одиницями є сантиметр, грам, секунда. Одиниця заряду в цій системі (позначається СГСЕq) вводиться так, щоб коефіцієнт пропорціональностіk в законі Кулона (1.1) дорівнював одиниці. Два точкових заряди, кожен з яких дорівнює 1 СГСЕq. перебуваючи на відстані 1 см один від одного, взаємодіють з силою в 1 дину. Діна - це одиниця сили в системі СГС. Вона дорівнює силі, яка тілу масою 1 г повідомляє прискорення 1 см / с 2.
Електричні заряди створюють у оточуючому просторі електричне поле, за допомогою якого і здійснюється взаємодія зарядів. Основною характеристикою електричного поля в будь-якій точці простору є напруженість.
Напруженість електричного поляE це векторна величина, що дорівнює відношенню сілиF, що діє на електричний зарядq, помещеннийв дану точку, до величини цього заряду
Використовуючи напруженість, співвідношення (1.2) і (1.3) можна записати у вигляді
де E (q1) напряженность, створювана зарядомq1 в точці, де знаходиться зарядq2. АE (q2) напряженность, створювана зарядомq2 в точці, де знаходиться зарядq1.
Порівнюючи формули (1.1-3) і (1.5), знайдемо вирази для напруженості поля, створюваного точковим зарядом q в точці, що знаходиться на расстоянііr від заряду
в системі СІ (1.6)
в гаусом системі. (1.7)
В системі СІ одиниця напруженості поля вольт на метр (В / м). З (1.4) випливає 1 В / м = (1 Н) / (1 Кл). Визначення вольта буде дано пізніше. Треба сказати, що логіка найменувань і зв'язків між одиницями в системі СІ вельми своєрідна, тому іноді доводиться вживати позначення, виражені через одиниці, яких ми ще не вводили.
Електричне поле зручно графічно зображати за допомогою так званих силових ліній. іліліній напруженості. Вони являють собою криві, напрямок дотичної до яких в будь-якій точці збігаються з напрямом вектораЕ в цій точці. Лінії напруженості електростатичного поля починаються на позитивних зарядах і закінчуються на негативних.
Силові лінії відокремленого точкового заряду є симетрично розподілені радіальні прямі, які виходять із точки, де розташований заряд. Проведемо подумки досить багато таких ліній і позначимо їх повне число черезN. Так як лінії напруженості в просторі між зарядами безперервні, то число ліній, що виходять назовні з будь-якої замкнутої поверхні, що охоплює заряд, равноN.
Тоді густота ліній на відстані r від заряду, тобто число ліній, які перетинають одиницю площі поверхні сфери радіусаr. равнаN / (4r 2). Порівнюючи це з виразом (1.6-7) для напруженості поля точкового заряду, можна переконатися, що густота ліній і абсолютна величина напруженості пропорційні один одному.
Напруженість однорідного поля (створюваного, наприклад, рівномірно зарядженої протяжної пластиною) у всіх точках однакова за величиною і напрямком, тому його силовими лініями є паралельні прямі.
Експерименти показують, що сила взаємодії двох зарядів не змінюється при наявності третього заряду. Скільки б зарядів ні входило в систему, закон Кулона (рівняння (1.1-3)) можна використовувати для обчислення сил взаємодії кожної пари.
Звідси випливає принцип суперпозиції: напруженість поля, створювана декількома зарядаміqi, дорівнює векторній сумі напруженостей полейЕi, створюваних каждимi-тим зарядом окремо
Принцип суперпозиції означає, що присутність інших зарядів не позначається на електричному полі, створюваному даними зарядом.
Мал. 1.1 ілюструє застосування принципу суперпозиції при знаходженні напруженості поля Е. створюваного позитивним зарядомQ1 і негативним зарядомQ2 в точці, що знаходиться на расстоянііr1 від першого заряду і наr2 від другого:
де Е1 іЕ2 - напруженості полів, створюваних кожним із зарядів окремо.
Використовуючи теорему косинусів, знайдемо модуль Е.
.