Побудова кодів Хеммінга базується на принципі перевірки на парність ваги W (числа одиничних символів) в інформаційній групі кодового блоку.
Пояснимо ідею перевірки на парність на прикладі найпростішого коригуючого коду, який так і називається кодом з перевіркою на парність або кодом з перевіркою за паритетом (рівності).
В такому коді до кодовою комбінаціям безізбиточного первинного довічного m - розрядного коду додається один додатковий розряд (символ перевірки на парність, званий перевірочним, або контрольним). Якщо число символів "1" вихідної кодової комбінації парне, то в додатковому розряді формують контрольний символ 0, а якщо число символів "1" непарне, то в додатковому розряді формують символ 1. В результаті загальне число символів "1" в будь-який передається кодової комбінації завжди буде парним.
Таким чином, правило формування перевірочного символу зводиться до наступного:
,
де i - відповідний інформаційний символ (0 або 1), m - загальне їх число а під операцією "" тут і далі розуміється складання поmod2. Очевидно, що додавання додаткового розряду збільшує загальне число можливих комбінацій удвічі в порівнянні з числом комбінацій вихідного первинного коду, а умова парності розділяє всі комбінації на дозволені і недозволені. Код з перевіркою на парність дозволяє виявляти одиночну помилку при прийомі кодової комбінації, так як така помилка порушує умову парності, переводячи дозволену комбінацію в заборонену.
Критерієм правильності прийнятої комбінації є рівність нулю результату S підсумовування поmod2 всехn символів коду, включаючи перевірки сімволk1. При наявності одиночної ошібкіS приймає значення 1:
.
Цей код є (m + 1, m) - кодом, або (n, n -1) - кодом. Мінімальна відстань коду дорівнює двом (dmin = 2), і, отже, ніякі помилки не можуть бути виправлені. Простий код з перевіркою на парність може використовуватися тільки для виявлення (але не виправлення) одноразових помилок.
Збільшуючи число додаткових перевірочних розрядів і формуючи за певними правилами перевірочні символи k. рівні 0 або 1, можна підсилити коригувальні властивості коду так, щоб він дозволяв не тільки виявляти, але і виправляти помилки. На цьому і засноване побудова кодів Хеммінга.
Коди Хеммінга. Розглянемо ці коди, що дозволяють виправляти одиночну помилку, за допомогою безпосереднього опису. Для кожного числа перевірочних сімволовk = 3,4,5 ... існує класичний код Хеммінга з маркуванням
тобто - (7,4), (15,11), (31,26) ...
При інших значеннях числа інформаційних символів m виходять так звані усічені (укорочені) коди Хеммінга. Так, для міжнародного телеграфного коду МТК-2. має 5 інформаційних символів, буде потрібно використання коригуючого коду (9,5), що є усіченим від класичного коду Хеммінга (15,11), так як число символів в цьому коді зменшується (коротшає) на 6. Для прикладу розглянемо код Хеммінга (7,4 ), який можна сформувати і описати за допомогою кодера, представленого на рис.13.1. У найпростішому варіанті при заданих чотирьох (m = 4) інформаційних символах (i1, i2, i3, i4) будемо вважати, що вони згруповані на початку кодового слова, хоча це і не обов'язково. Доповнимо ці інформаційні символи три перевірних символами (k = 3), задаючи їх наступними рівностями перевірки на парність, які визначаються відповідними алгоритмами. Відомо, що кодова відстань дорівнює мінімальному числу перевірок, в які входить інформаційний символ плюс один. В даному кодеdmin. Отже кожен інформаційний символ повинен входити мінімум в два пункти. Визначимо правило формування перевірочних символів наступний чином:
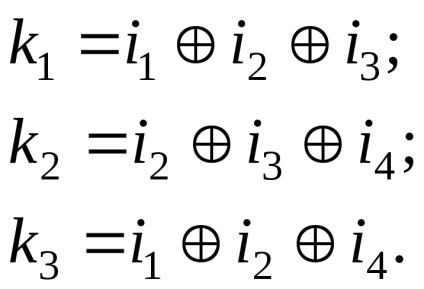
Відповідно до цього алгоритмом визначення значень перевірочних символів ki на ріс.13.3 наведені всі можливі 16 кодових слів (7,4) - коду Хеммінга.
На рис. 13.2пріведена схема декодера для (7,4) - коду Хеммінга, на вхід якого надходить кодове слово
.
Апостроф означає, що будь-який символ слова може бути спотворений перешкодою в каналі передачі.
У декодере в режимі виправлення помилок будується послідовність:

Трёхсімвольная послідовність (s1. S2. S3) називається синдромом. Термін "синдром" використовується і в медицині, де він позначає поєднання ознак, характерних для певного захворювання. В даному випадку сіндромS = (s1. S2, s3) являє собою поєднання результатів перевірки на парність відповідних символів кодової групи і характеризує певну конфігурацію помилок (вектор помилок).
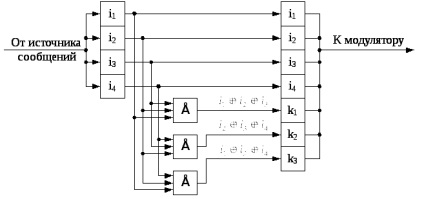
Рис.13.1. Кодер для простого (7,4) - коду Хеммінга
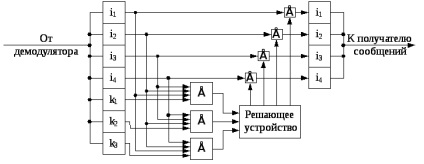
Рис.13.2. Декодер для простого (7,4) - коду Хеммінга
Таким чином, код (7,4) дозволяє виправити всі поодинокі помилки. Проста перевірка показує, що кожна з помилок має свій єдиний синдром. При цьому можливе створення такого цифрового коректора помилок (дешифратора синдрому), який за відповідним синдрому виправляє відповідний символ в прийнятій кодовій групі. Після внесення виправлення перевірочні символи ki можна на вихід декодера (рис.13.2) не виводити. Дві або більше помилки перевищують можливості коригуючого коду Хеммінга, і декодер буде помилятися. Це означає, що він буде вносити неправильні виправлення і видавати спотворені інформаційні символи.
Ідея побудови подібного коригувального коду, природно, не змінюється при перестановці позицій символів в кодових словах. Всі такі варіанти також називаються (7,4) - кодами Хеммінга.
Розширені коди Хеммінга будуються в результаті доповнення кодів сdmin = 3 спільною перевіркою кожної з кодових комбінацій на парність, тобто ще одним перевірочним символом. Це дозволяє збільшити мінімальну кодову відстань доdmin = 4.
Для продовження скачування необхідно зібрати картинку: