Ковзаючим режимом називається режим роботи релейного системи, що характеризується коливальним рухом зображає точки вздовж лінії перемикання. Чим сильніше вплив похідною в колі зворотного зв'язку, тим більше повертаються лінії перемикання реле проти годинникової стрілки. При цьому інтенсивність загасання перехідного процесу зростає. У тому випадку, коли в точці перемикання кут нахилу лінії перемикання стає рівним нахилу або менше кута нахилу дотичній до фазової траєкторії, по якій рухається зображає точка після перемикання реле, виникають умови існування ковзного режиму [10].
Розглянемо виникнення ковзного режиму в нелінійній системі, зображеній на рис. 2.20, а, з ідеальним реле при відсутності зовнішнього впливу і при заданих початкових умовах x0 ¹ 0 і y0 = 0.
Нехай початковий стан системи задано точкою (x0. 0) (рис. 2.25), від якої зображає точка переміщається по фазової траєкторії типу 1 до зустрічі з лінією перемикання AB в точці C. У цій точці відбувається перемикання реле і зображає точка буде переміщатися по фазової траєкторії типу 2 до точки D. у точці D відбувається перемикання реле в іншу сторону, після чого зображає точка буде переміщатися по фазової траєкторії типу 1. Але як тільки збільшиться результуючий сигнал зворотного зв'язку, відбудеться перемикання реле і зображає точка буде переміщатися по фазової траєкторії типу 2 і так далі, тобто зображає точка, підійшовши до цього відрізка лінії перемикання - відрізку ковзання, не зможе піти з нього.
Таким чином, що зображає точка, досягнувши точки D, безперервно переходить з траєкторії типу 1 на траєкторію типу 2 і назад, як би ковзаючи вздовж лінії перемикання і асимптотично наближаючись до точки рівноваги 0.
Як видно з рис. 2.25, ковзний режим можливий на тих ділянках, де фазова траєкторія типу 2 проходить нижче лінії перемикання AB (після точки D). При початковому положенні зображає точки (x02. 0) після її приходу по траєкторії типу 1 в точку на лінії перемикання D відразу починається ковзний режим. При початковому положенні зображає точки (x03. 0) ковзний режим має місце після перемикання реле, коли зображає точка ковзає по лінії перемикання AB в четвертому квадранті. В останньому випадку перехідний процес має перерегулювання.

Мал. 2.25. Фазові траєкторії релейного системи
У розглянутому прикладі передбачається, що перемикання реле відбувається миттєво, в результаті частота перемикань нескінченно велика, а амплітуда коливань нескінченно мала. Такий ковзний режим називається граничним. Якщо врахувати неоднозначність характеристики або зону нечутливості, то перемикання реле при ковзному режимі відбувається з кінцевою частотою, а амплітуда коливань відрізняється від нуля.
У граничному ковзному режимі релейний елемент можна замінити еквівалентним лінійним безінерційним ланкою з коефіцієнтом передачі, які прагнуть до нескінченності (kp ® ¥). Тоді еквівалентна передатна функція системи, відповідна структурній схемі, наведеній на рис. 2.20, а, буде
Отже, для граничного змінного режиму релейний систему можна представити еквівалентною структурною схемою у вигляді інтегруючого ланки, охопленого зворотним зв'язком, або просто у вигляді аперіодичної ланки першого порядку.
При початковому положенні системи x01 (точка M0 на рис. 2.25) після перемикання реле в точці M1 зображає точка по фазової траєкторії типу 2 приходить в початок координат, що характеризує стан спокою. При цьому перехідний процес буде мати мінімальний час, а режим роботи системи буде оптимальним за швидкодією. При заданій постійній часу коректує ланцюга зворотного зв'язку Toc такий режим буде існувати тільки для певної групи початкових значень, коли зображає точка в початковий момент часу виявляється на траєкторії M0 M1 0. що проходить через початок координат; у всіх інших випадках буде мати місце ковзний режим або відразу після перемикання реле, або після декількох перемикань.
Для того щоб процес при будь-яких початкових умовах був оптимальним за швидкодією, лінією перемикання повинна бути сама фазова траєкторія, що проходить через початок координат. Така крива лінія перемикання свідчить про нелінійному характері впливу коректує зворотного зв'язку. Лінія перемикання не відноситься до фазовим траєкторіях. Але можна зробити так, що вона буде збігатися з однією з фазових траєкторій. Тоді процес в системі буде складатися з двох частин: підхід до лінії перемикання по одній з траєкторій, вибір якої залежить від початкових умов, і рух по лінії перемикання до стану рівноваги.
Наочне уявлення про сукупності оптимальних процесів при різних початкових умовах дає фазовий портрет, наведений на рис. 2.26.

Мал. 2.26. Фазовий портрет оптимальної за швидкодією системи:
AB - лінія перемикання
При побудові оптимальних за швидкодією систем основним завданням є формування функції управління, що характеризує перемикання релейного елемента. На рис. 2.27 приведена структурна схема системи з нелінійним зворотним зв'язком.
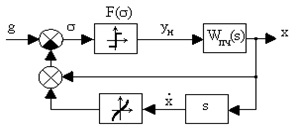
Мал. 2.27. Структурна схема оптимальної за швидкодією системи
У загальному випадку оптимальна по швидкодії система може містити обчислювальний пристрій, яке формує функцію нелінійного зворотного зв'язку, логічні елементи і мати змінну структуру.