
11. Креслення і аксонометричні проекції геометричних тіл
Отже, ви вже знаєте, що форма більшості предметів являє собою поєднання різних геометричних тіл або їх частин. Отже, для читання і виконання креслень потрібно знати, як зображуються геометричні тіла.
11.1. Проектування куба і прямокутного паралелепіпеда. Куб розташовують так, щоб його межі були паралельні площинам проекцій. Тоді вони изобразятся на паралельних їм площинах проекцій в натуральну величину - квадратами, а на перпендикулярних площинах - відрізками прямих (рис. 76).
Проекціями куба є три рівних квадрата.
На кресленні куба і паралелепіпеда вказують три розміри: довжину, висоту і ширину.
На малюнку 77 деталь утворена двома прямокутними паралелепіпедами, що мають по дві квадратні межі. Зверніть увагу, як нанесені на кресленні розміри. Плоскі поверхні відзначені тонкими пересічними лініями.
Завдяки умовному знаку # 9633; форма деталі ясна і по одному виду.
11.2. Проектування правильних трикутної і шестикутної призм. Підстави призм, паралельні горизонтальній площині проекцій, зображуються на ній в натуральну величину, а на фронтальній і профільній площинах - відрізками прямих. Бічні грані зображуються без спотворення на тих площинах проекцій, яким вони паралельні, і у вигляді відрізків прямих на тих, яким вони перпендикулярні (рис. 78). Грані, нахилені до площин проекцій, зображуються на них спотвореними.
Розміри призм визначаються їх висотою і розмірами фігури підстави. Штрихпунктирними лініями на кресленні про-ведені осі симетрії.
Будувати ізометричні проекції призми починають з підстави. Потім з кожної вершини підстави проводять перпендикуляри, на яких відкладають відрізки, рівні висоті, і через отримані точки проводять прямі, паралельні ребрам підстави.
Креслення в системі прямокутних проекцій також починають виконувати з горизонтальної проекції.
11.3. Проектування правильної чотирикутної піраміди. Квадратну підставу піраміди проектується на горизонтальну площину Н в натуральну величину. На ньому діагоналями зображуються бічні ребра, що йдуть від вершин підстави до вершини піраміди (рис. 79).
Фронтальна і профільна проекції піраміди - трикутник.
Розміри піраміди визначаються довжиною b двох сторін її заснування і висотою h.
Изометрическую проекцію піраміди починають будувати з підстави. З центру отриманої фігури проводять перпендикуляр, відкладають на ньому висоту піраміди і з'єднують отриману точку з вершинами підстави.
11.4. Проектування циліндра і конуса. Якщо кола, що лежать в основах циліндра і конуса, розташовані паралельно горизонтальній площині Н, їх проекції на цю площину будуть також колами (рис. 80, б і д).
Фронтальна і профільна проекції циліндра в цьому випадку - прямокутники, а конуса - трикутник.
Зауважте, що на всіх проекціях слід наносити осі симетрії, з проведення яких і починають виконання креслень циліндра і конуса.
Фронтальна і профільна проекції циліндра однакові. Те ж можна сказати про проекціях конуса. Тому в даному випадку профільні проекції на кресленні зайві. Крім того, завдяки знаку 0 можна уявити форму циліндра по одній проекції (рис. 81). Звідси випливає, що в подібних випадках немає необхідності в трьох проекціях. Розміри циліндра і конуса визначаються їх висотою h і діаметром підстави d.
Способи побудови ізометричної проекції циліндра і конуса однакові. Для цього проводять осі х і у, на яких будують ромб. Сторони його рівні діаметру підстави циліндра або конуса. В ромб вписують овал (див. Рис. 66).
11.5. Проекції кулі. Все проекції кулі - кола, діаметр яких дорівнює діаметру кулі (рис. 82). На кожній проекції проводять центрові лінії.
Завдяки знаку діаметр куля можна зображувати в одній проекції. Але якщо за кресленням важко відрізнити сферу від інших поверхонь, додають слово «сфера», наприклад: «Сфера дмаметр 45».
11.6. Проекції групи геометричних тіл. На малюнку 83 дано проекції групи геометричних тіл. Чи можете ви сказати, скільки геометричних тел входить в цю групу? Які це тіла?
Розглянувши зображення, можна встановити, що на ньому дані конус, циліндр і прямокутний паралелепіпед. Вони по-різному розташовані щодо площин проекцій і один одного. Як саме?
Ось конуса перпендикулярна горизонтальної площини проекцій, а вісь циліндра - профільної площини проекцій. Дві грані паралелепіпеда паралельні горизонтальній площині проекцій. На профільної проекції зображення циліндра знаходиться праворуч від зображення паралелепіпеда, а на горизонтальній - нижче. Це означає, що циліндр розташований попереду паралелепіпеда, тому частина паралелепіпеда на фронтальній проекції показана штриховою лінією. По горизонтальній і профільної проекцій можна встановити, що циліндр стосується паралелепіпеда.
Фронтальна проекція конуса стосується проекції паралелепіпеда. Однак, судячи з горизонтальної проекції, паралелепіпед не стосується конуса. Конус розташований лівіше циліндра і паралелепіпеда. На профільної проекції він частково їх закриває. Тому невидимі ділянки циліндра і паралелепіпеда показані штриховими лініями.
20. Як зміниться профільна проекція на малюнку 83, якщо з групи геометричних тіл видалити конус?
1. На столі лежать шашки, як показано на малюнку 84, а. Порахуйте за кресленням, скільки шашок перебуває в перших ближніх до вас стовпчиках. Скільки всього шашок лежить на столі? Якщо вам важко порахувати їх за кресленням, спробуйте спочатку взяти і скласти шашки в стовпчики, користуючись кресленням. Тепер спробуйте правильно виконати завдання.
2. На столі в чотири стовпчики (рис. 84, б) розташовані шашки. На кресленні вони показані двома проекціями. Скільки шашок на столі, якщо чорних і білих порівну? Для вирішення цього завдання потрібно не тільки знати правила проектування, але і вміти логічно міркувати.
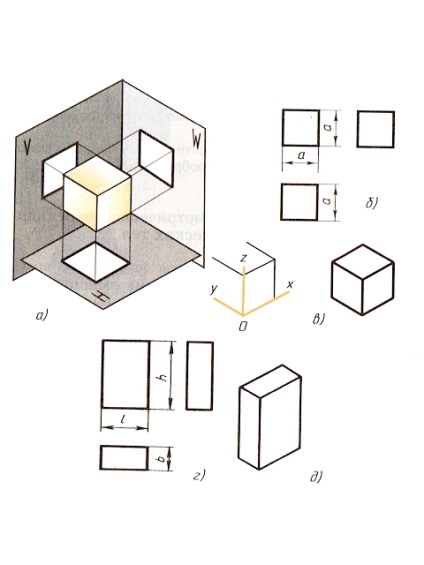
Мал. 76. Куб і паралелепіпед: а - проектування; б, г креслення в системі прямокутних проекцій; в, д - ізометричні проекції
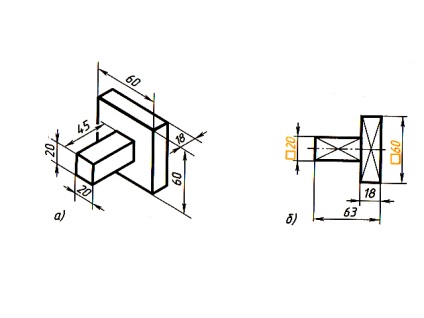
Мал. 77. Зображення деталі в одному виді
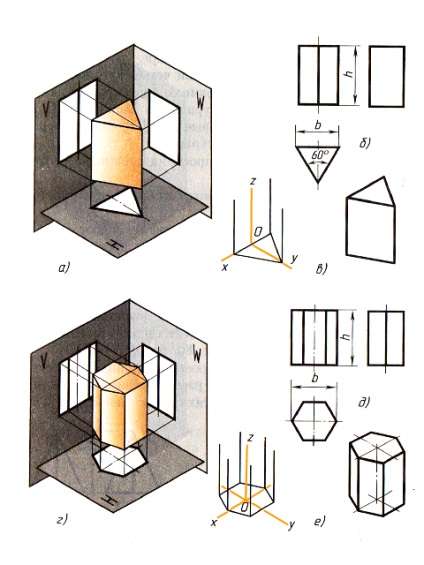
Мал. 78. Призми:
а, г - проектування; б, д - креслення в системі прямокутних проекцій; в, е - ізометричні проекції
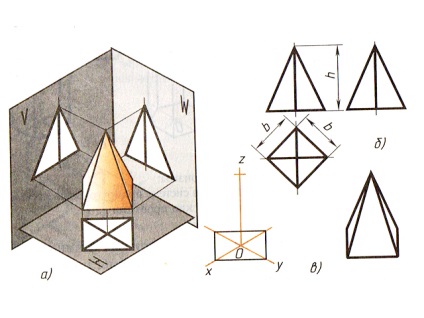
Мал. 79. Піраміда: а - проектування; б - креслення в системі прямокутних проекцій; в - ізометрична проекція
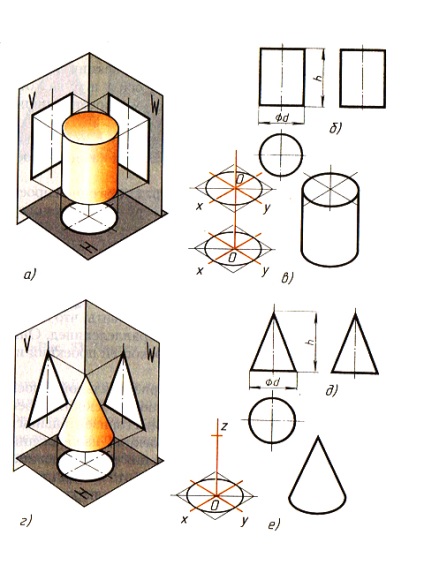
Мал. 80. Циліндр і конус: а, г - проектування; 6, д - креслення в системі прямокутних проекцій; в, с - ізометричні проекції
Мал. 81. Зображення циліндра в одному виді
Мал. 82. Проекції кулі
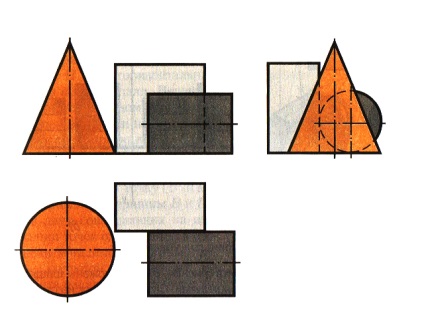
Мал. 83. Креслення проекції групи геометричних тіл
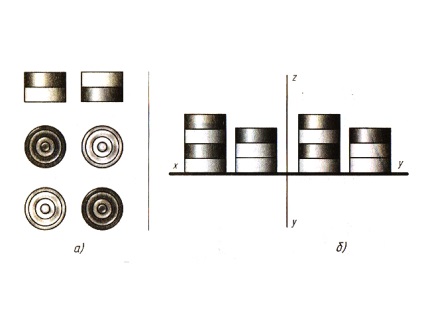
Мал. 84. Завдання для вправ



