
Ми всі знаємо що таке крива. Ось кілька прикладів.
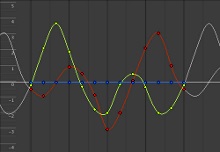
В іграх криві Безьє іноді корисні для опису шляху: гоночний шлях на трасі в гоночної грі, або лінії в іграх з малюванням ліній, таких як Flight Control, або зациклена траєкторія польоту метелика, що що живе в світі RPG.

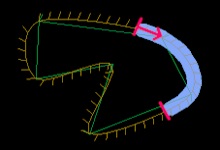

Криві Безьє так популярні, тому що їх математичне опису дуже компактно, інтуїтивно зрозуміло і елегантно. Їх легко обчислити, легко використовувати в більш високих вимірах (3D і вище), і можуть бути пов'язані один з одним, щоб представити будь-яку форму яку ви тільки можете собі уявити.
У цьому керівництві я дам вам інструкції, необхідні для реалізації алгоритмів, щоб можна було використовувати криві Безьє в своїх іграх.
Почнемо з математики. Математично ми можемо описати криву Безьє на функцію. Функція приймає параметр. Значення функції є точка на кривій; вона залежить від параметра. і від безлічі точок, які називаються контрольними точками. Перша і остання контрольні точки є кінцями кривої. Як правило, крива не проходить через інші контрольні точки.
Значення може коливатися від 0 до 1. Значення 0 відповідає початковій точці кривої, значення 1 відповідає кінцевій точці кривої. Значення в проміжку відповідають іншим точкам на кривій.
Ось приклад найпростішого типу кривої Безьє, відрізок:
А ось скорочена назва для двох рівнянь, які дають роздільні координати:

Точки і є контрольними точками. Коли. права частина рівняння дорівнює першій контрольній точці - початку відрізка. Коли. отримуємо точку. другу контрольну точку - кінець відрізка.
Для більш цікавих форм нам потрібно більше контрольних точок. Кількість контрольних точок визначає ступінь кривої. Дві контрольні точки необхідні для лінійних (перша ступінь) кривих, таких як відрізок вище. Для другого ступеня, або квадратичних кривих, нам потрібні три контрольні точки.
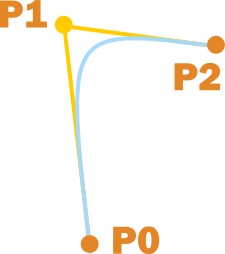
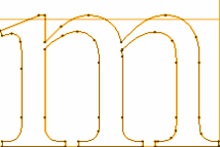
Кубічні криві (або криві третього ступеня) є найбільш часто іспользуюемимі, і тому в цьому посібнику ми будемо обговорювати саме кубічні криві. Для їх побудови потрібно чотири контрольні точки, і можливо ви вже добре знайомі з їх використанням в пакетах векторної графіки (так, ті самі кружечки які використовуються для зміни форми кривих в програмах Freehand або Inkscape і є нашими контрольними точками).
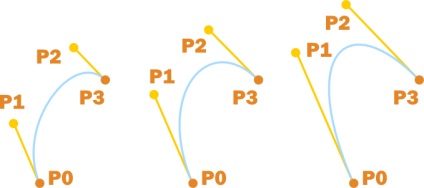
Жовті лінії протягнуті в тому ж напрямку, що і дотичні на кінцях крівой.Чем далі розташовані ці жовті сегменти, тим сильніше "натягнута" крива у напрямку дотичних.
Формула для кубічних кривих Безьє:
Ви навряд чи будете мати потребу в більш високих ступенях кривої. Якщо це так, то формула проста, але вимагає деяких знань біноміальні коефіцієнтів. Ви можете знайти подробиці в одному з джерел в кінці статті.
В геометрії завжди знайдеться більше проблем, ніж ви спочатку могли подумати, що може привести до тривалого пошуку помилок.
Ось правильні 2D криві Безьє:
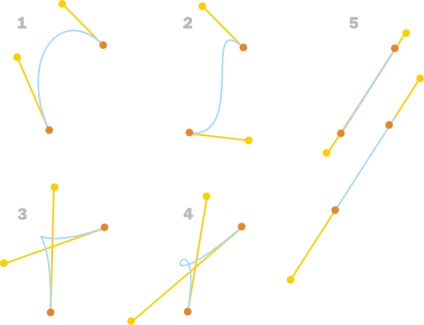
Всі кінцеві точки на однаковій відстані одна від одної. 1. Крива без перегину, залома або петлі. 2. Крива з перегином, без заломів або петель. 3. Крива з заломом. 4. Крива з петлею. 5. Пряма лінія. (В точці перегину крива змінює напрямки згину)
Вироджений випадок 5 є найскладнішим. Можуть бути наступні варіанти:
- немає перекриттів
- крива заламується двічі на одному або обох кінцях
- крива заламується тричі трійка десь між кінцями
У 3D, петлі і переломи доставляють менше проблем, так як вони проявляються лише в тому випадку, коли всі точки лежать в одній площині. У 3D завжди можна змінити напрямок руху прямий (особливо для таких випадків як 2, 4 і 5).
Математичну формулу нескладно перевести в код. Нижче приводиться реалізація алгоритму, в якій вже проведена певна оптимізація шляхом збереження і повторного використання проміжних результатів.
Код наводиться на мові C #, але перевести на Java, C + + і більшість інших мов не повинно принести особливих проблем.
(Наступні функції будуть працювати і в 2D, якщо Vector3 замінити на Vector2.)