Синусоїда. Плоска крива, що характеризує зміну величини синуса кута в залежності від величини кута, називається синусоїдою. Для побудови синусоїди задану окружність ділять на кілька рівних частин (рис. 1). На стільки ж рівних частин ділять вісь синусоїди, довжину якої приймають рівною довжині окружності 2ПR. З точок розподілу, підіймали до осі перпендикуляри, на яких відкладають ординати, рівні відповідним відрізкам синусів. Отримані точки I, II, III і ін. З'єднують плавною кривою. У разі потреби крива може бути продовжена за точку VIII. При побудові гвинтових ліній, часто зустрічаються в техніці, застосовується стисла синусоїда, у якій крок менше довжини кола.
Мал. 1. Побудова синусоїди
Спіралі. Плоска крива, яку отримують при русі точки, що обертається навколо деякого центру і одночасно віддаляється від нього по деякому закону, називається спіраллю. Якщо видалення від центру пропорційно кутовому переміщенню точки, то крива називається спіраллю Архімеда. Розміри кривої залежать від величини кроку спіралі OVIII (рис. 2). Для побудови кривої проводять коло радіусом, рівним кроку спіралі. Ділять крок і окружність на однакове число рівних частин. Від центру Про по радіусах відкладають одну, дві, три і т. Д. Частини, отримуючи точки спіралі I, II, III і ін.
Криві, виражені рівняннями. Закономірні криві часто задають рівняннями. Нехай, наприклад, потрібно побудувати криву, задану рівнянням х = у 2 + 2 (рис. 3). Проводять координатні осі х і у. Підставляють в рівняння замість у величини: 0, 1, 2, 3, 4 і т. Д. Знаходять, чому буде дорівнює при цьому величина х. У першому випадку х = 2, у другому х = 3, в третьому - б, в четвертому - 11 і т. Д. Відкладають по осях х та у відповідні величини і на перетині перпендикулярів знаходять точки I, II, III, IV, V та ін.
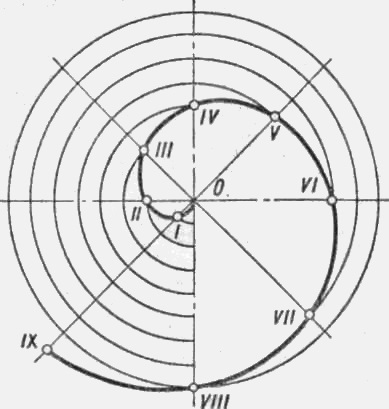
Мал. 2. Побудова спіралі Архімеда
Мал. 3. Побудова кривої за рівнянням