ЗАВДАННЯ 7. Знайти об'єм тіла, обмеженого зазначеними поверхнями.
Наведемо рішення двох завдань на обчислення об'ємів тіл, розглядаючи тіла з різною геометрією поверхні.
1). Тіло обмежена двома поверхнями: параболоїдом і площиною. Зобразимо це тіло на кресленні (ріс.75).
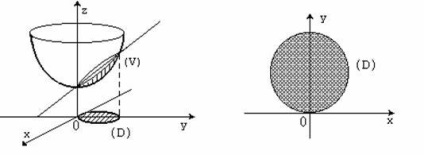
Дане тіло є циліндричні брусом (ріс.72); бокова поверхня виродилася в лінію перетину заданих поверхонь. Знайдемо область, в яку тіло проектується на площину, для чого з рівнянь поверхонь, що обмежують тіло, слід виключити змінну (тобто зробити ортогональное проектування):
Таким чином, областю () є коло з центром в точці (0; 1) радіусу = 1 (див. Ріс.75).
Обсяг тіла може бути обчислений за допомогою потрійного інтеграла за формулою. У декартовій системі координат потрійний інтеграл записується через повторний наступним чином:
звідки видно, що його обчислення пов'язане зі значними труднощами (на завершальній стадії обчислення повторного інтеграла).
Запишемо інтеграл в циліндричній системі координат, з якою декартова система пов'язана формулами
Якобіан перетворення. Формула переходу (в інтегралі) має вигляд
Запишемо рівняння параболоїда і площини в циліндричній системі координат:
Для кола маємо; кут, очевидно, необхідно змінювати в межах від 0 до. Таким чином ,
Циліндричний брус проектується на площину в криволінійну трапецію (D): 0 # 61603; # 61472; x # 61603; # 61472; 1, 0 # 61603; # 61472; y # 61603; # 61472; . Перетворимо потрійний інтеграл в повторний і обчислимо його:
Зауваження. В циліндричній системі координат обчислення спрощуються:
ЗАВДАННЯ 11. Обчислити криволінійний інтеграл
за формулою Гріна; замкнутий контур () складається з двох кривих: і (див. рис. 80).
ЗАВДАННЯ 12. Обчислити масу дуги кривої () при заданій щільності:
1) Розглядається випадок параметричного завдання кривої (). Масу плоскої кривої можна обчислити за допомогою криволінійного інтеграла першого роду:. Для обчислення його потрібно звести до певного інтеграла від функції однієї змінної по відрізку за формулою:
Робота сили по переміщенню матеріальної точки одиничної маси є лінійний інтеграл уздовж дуги від точки до точки
Останній інтеграл є криволінійний інтеграл другого роду по просторової кривої. Його обчислення зводиться до обчислення певного інтеграла, для чого криву треба уявити в параметричної формі (умовою завдання крива задана у вигляді лінії перетину поверхні кругового циліндра з площиною, см. Ріс.81).
Приклад. Знайдемо, де - модуль радіус-вектора.
За формулою 5 з цієї рівності випливає:
Ми отримали формулу для обчислення гдаріента радіальної функції.
Розглянемо тепер поверхню рівня скалярного поля, тобто поверхню, що задається рівнянням. Припустимо, що - безперервно диференціюється функція від. Тоді рівняння дотичної площини в точці, що лежить на цій поверхні, має вигляд.
Координати вектора градієнта є коефіцієнти цього рівняння. Тому - нормаль до дотичної площини в т. І, за визначенням, нормаль до самої поверхні рівня в цій точці.
Потік вектора через поверхню. Дивергенція векторного поля. Нехай - векторне поле, - двостороння поверхню. Нехай обрана сторона, тобто нормаль. Назвемо - потоком вектора через поверхню в зазначену бік.
Цей термін збігається з наступною гідродинамічної завданням. Нехай - вектор швидкості течії рідини в момент. Порахуємо, скільки рідини пройде через малу частину поверхні за момент часу. Цей обсяг рідини являє собою циліндр з основою і висотою, тобто цей обсяг дорівнює.
Тоді для всієї воверхності отримаємо. Таким чином, потік являє собою швидкість зміни кількості протікає через рідини в даний момент часу.