Лініями переходу в курсі креслення називаються лінії, за якими перетинаються між собою поверхні.
Теорії побудови ліній переходу для різних поверхонь приділяється багато уваги в курсах нарисної геометрії, тут це питання розглядається коротко.
У разі перетину осей двох тіл обертання застосовується спосіб кульових поверхонь. Розглянемо його на прикладі побудови перетину двох циліндрів, осі яких лежать в одній площині.
Нехай дано: барабан діаметром D, циліндричний штуцер діаметром d і точка 0 перетину осей обох циліндрів (фіг. 170). Потрібно побудувати лінію переходу.
Точки 1 і 5 легко визначаються: вони лежать на перетині крайніх утворюють малого циліндра з верхньою твірною великого. Кожна наступна проміжна точка лінії переходу буде визначатися окружністю перетину кулі з будь-яким з циліндрів. На наведеному кресленні ці окружності зображатимуться: для малого ціліндра- горизонтальними прямими mn, ba і т. Д. А для великого-вертикальними ks, c4, e2 і т. Д. Перетин цих кіл і дає шукані точки лінії переходу. Наприклад, куля радіуса Ос перетне малий циліндр по колу, проекцією якої є пряма ba, а великий-за дугах кола 4c6 і 2e8. Перетин цих дуг дає точки 4 і 6, 2 і 8.
Для визначення нижніх точок лінії переходу, т. Е. Точок 3 і 7, побудуємо куля радіусом D / 2- дотичний до великого циліндру. Проекція цієї кулі-окружність з радіусом D / 2 - перетинає продовження
крайніх утворюють малого циліндра в двох точках n і m і стосується великого-по колу ks. Перетин mn і ks дає шукані точки: З-на передній стороні бічної поверхні циліндра, 7-на протилежному боці. Отримані точки з'єднуємо кривій однакової товщини.
Справа на цьому ж кресленні зображений штуцер такого ж діаметру, як і в попередньому прикладі, з тією лише різницею, що він з'єднується з барабаном не впритул, а по кривій радіус R. Побудова точок
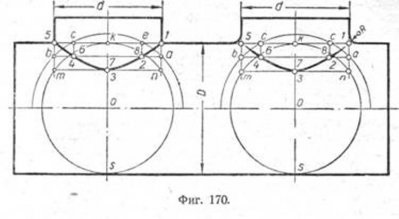
лінії переходу виконується так само, як і для штуцера, зображеного ліворуч. Лінія переходу, в міру підходу до точок 1 і 5, змінює свою товщину і як би зводиться нанівець. Доцільність застосування способу кульових перетинів очевидна. Завдання тут вирішується без додаткових проекцій.
Якщо геометричні осі тіл обертання не перетинаються, то в цьому випадку треба користуватися способом послідовного знаходження точок зустрічі утворюють однієї поверхні з іншого. Розглянемо випадок
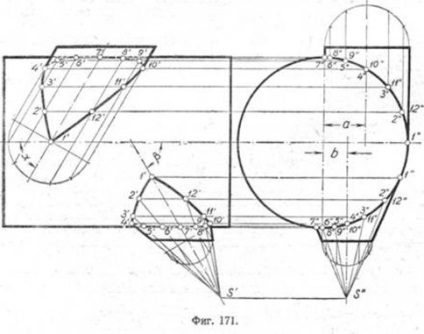
перетину циліндричного і конічного штуцерів, осі яких складають з віссю барабана кути нахилу а й. і не перетинаються з віссю основного циліндра (фіг. 171). Для побудови лінії переходу циліндричного штуцера, вісь якого нахилена до барабану під кутом а, ділимо коло перетину, перпендикулярного до його осі, на деяке число рівних частин, наприклад на 12. Проводимо утворюють через точки поділу на вертикальній і профільної площинах проекцій і нумеруем їх. Утворюють штуцера перетинаються на профільній проекції з корпусом барабана в точках 1 ", 2", 3 ". 12". Переносимо ці точки на відповідні утворюють вертикальної проекції. Отримано-ні точки 1 ', 2', 3 'і т. Д. З'єднуємо між собою спочатку від руки, а потім за лекалом. Ця крива і буде лінією переходу перетину циліндричного штуцера з барабаном.
Внизу, праворуч на кресленні, дано побудова лінії переходу перетину конічної штуцера з циліндром. На поверхні конуса про-водимо утворюють, віддалені один від одного на однаковій відстані. Точки їх зустрічі з поверхнею циліндра 1 ", 2", 3 ". 12" визначаємо на профільній проекції. Потім проекції знайдених точок переносимо на відповідні утворюють вертикальної проекції і з'єднуємо їх між собою спочатку від руки, потім за лекалом.
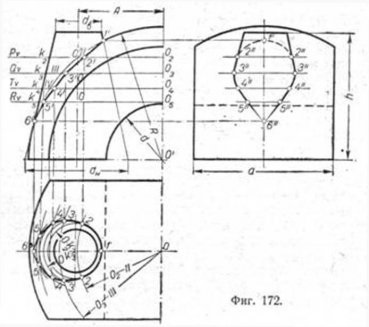
Точки 1 і 6 визначаються як точки перетину ліній контурів кулі і конуса на вертикальній площині проекцій. Для побудови інших точок шуканої кривої проводиться ряд горизонтальних площин, в проміжку
між точками 1 'і 6'. На кресленні їх сліди відзначені буквами Pv. Qv. Tv і Rv. Кожна з цих площин перетне одночасно і куля і конус по колах, які спроектують на горизонтальній площині в натуральну величину. Точки перетину кіл, що лежать в одній січної площини, і визначать проекції шуканих точок.
На всіх проекціях при обводке ліній переходу, підходячи до точки 6, слід зводити лінію нанівець, як це показано на кресленні.