лінійна незалежність
Лінійною комбінацією рядків el. e2. ek називають суму творів цих рядків на довільні дійсні числа:
e = l el + 2 e2 +. + k ek. де l. 2. k - довільні числа (коефіцієнти лінійної комбінації).
Рядки матриці el. e2. em називаються лінійно залежними. якщо існують такі числа l. 2. m. нерівні одночасно нулю, що лінійна комбінація рядків матриці дорівнює нульовий рядку:
l el + 2 e2 +. + m em = 0, де 0 = (0 0. 0).
Лінійна залежність рядків матриці означає, що хоча б один рядок матриці є лінійною комбінацією інших. Дійсно, нехай для визначеності останній коефіцієнт m 0. Тоді, розділивши обидві частини рівності на m. отримаємо вираз для останнього рядка. як лінійної комбінації інших рядків:
em = (l / m) el + (2 / m) e2 +. + (m-1 / m) em-1.
Якщо лінійна комбінація рядків дорівнює нулю тоді і тільки тоді, коли всі коефіцієнти дорівнюють нулю, тобто l el + 2 e2 +. + m em = 0 k = 0 k, то рядки називають лінійно незалежними.
Теорема про ранг матриці. Ранг матриці дорівнює максимальному числу її лінійно незалежних рядків або стовпців. через які можна лінійно висловити всі інші її рядки або стовпці.
Доведемо цю теорему. Нехай матриця А розміру m х n має ранг r (r (А) min). Отже, існує відмінний від нуля мінор r-го порядку. Всякий такий мінор будемо називати базисним. Нехай для визначеності це мінор
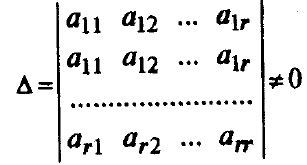
Рядки цього мінору також будемо називати базисними.
Доведемо, що тоді рядки матриці el. e2. er лінійно незалежні. Припустимо гидке, тобто одна з цих рядків, наприклад r-я, є лінійною комбінацією інших: er = l el + 2 e2 +. + r-1 er-1 = 0. Тоді, якщо відняти з елементів r-го рядка елементи 1-го рядка, помножені на l. елементи 2-го рядка, помножені на 2. і т.д. нарешті, елементи (r-1) -го рядка, помножені на r-1. то r-й рядок стане нульовою. При цьому за властивостями визначника вищенаведений визначник не повинен змінитися. і при цьому має дорівнювати нулю. Отримано протиріччя, лінійна незалежність рядків доведена.
Тепер доведемо, що будь-які (r + 1) рядків матриці лінійно залежні, тобто будь-який рядок можна виразити через базисні.
Доповнимо розглянутий раніше мінор ще одним рядком (i-й) і ще одним стовпцем (j-м). В результаті отримаємо мінор (r + 1) -го порядку, який за визначенням рангу дорівнює нулю:
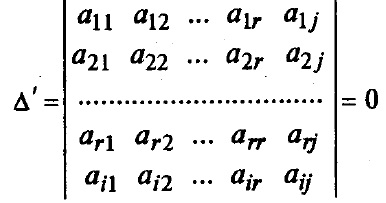
Розкладемо його за елементами j-го стовпця. Тут останнім алгебраїчне доповнення Аij збігається з базисним мінор 0 Аij 0. Тому можна розділити обидві частини останнього рівності на Аij. Це дозволить висловити з нього елемент:.
Якщо зафіксувати номер рядка (i), то отримаємо, що для будь-якого j елементи i-го рядка лінійно виражаються через елементи базисних рядків:, тобто будь-який рядок матриці є лінійною комбінацією базисних.