2.24. Лінійна згортка кінцевих послідовностей
Розглянемо дві кінцеві послідовності і довжини по і відліків, т. Е. Відмінна від нуля при, a - при. Лінійної або апериодической сверткой цих послідовностей називають послідовність, яка визначається співвідношенням
де і дорівнюють нулю поза відповідних інтервалів. На фіг. 2.30 наведені приклади послідовностей, і. Ясно, що послідовність є кінцевою і має довжину відліків.
Вище було показано, що, перемножая ДПФ двох кінцевих послідовностей і знаходячи зворотне ДПФ твори, отримуємо такий же результат, як при кругової згортку еквівалентних періодичних послідовностей, утворених з даних кінцевих послідовностей. Виходячи з цього (див. Також приклад на фіг. 2.29), можна досить просто отримати лінійну згортку двох кінцевих послідовностей. Згортка періодичних послідовностей періодична і має той же період, що і самі послідовності. Оскільки період згортки (фіг. 2.30) дорівнює отсчетам, то для отримання такого періоду при кругової згортку необхідно, щоб і містили по відліків, що досягається доповненням кожної з двох послідовностей відповідним числом нульових відліків. Після цього можна знайти -точкові ДПФ доповнених послідовностей, перемножити їх і виконати зворотне ДПФ твори.
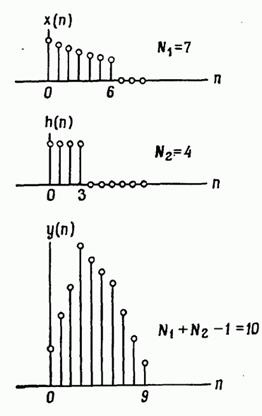
Фіг. 2.30. Лінійна (апериодическая) згортка.
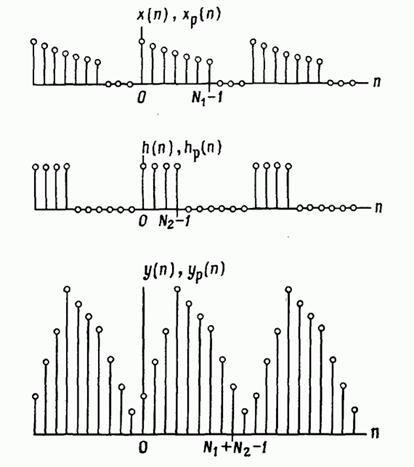
Фіг. 2.31. Обчислення лінійної згортки за допомогою кругової згортки.
В результаті виходить шукана згортка. На фіг. 2.31, що ілюструє ці операції, зображені еквівалентні періодичні послідовності, використовувані при обчисленні кругової згортки. Ясно, що доповнення вихідних послідовностей кінцевої довжини і нульовими отсчетами доводить період до потрібної величини і дозволяє усунути кругові накладення, характерні для кругової згортки. В результаті кожен період послідовності (фіг. 2.31) збігається з (фіг. 2.30). Розглянутий метод обчислення згортки двох кінцевих послідовностей із застосуванням алгоритму ДПФ називається швидкої сверткой на противагу методу прямого обчислення суми (2.165), званому прямої або повільної сверткой. Термін «швидка» застосовується тому, що ДПФ можна обчислити швидко і ефективно, використовуючи один з алгоритмів швидкого перетворення Фур'є (ШПФ). Можна показати, що навіть при помірних величинах (наприклад, близько 30) швидка згортка виявляється ефективніше прямої. Тому розглянута методика є важливим обчислювальним засобом при обробці сигналів.
Для практичних застосувань важливо відзначити, що в розглянутому вище прикладі розмір ДПФ не обов'язково обмежувати величиною. ДПФ можна виконувати з будь-якого числа відліків, що задовольняє умові. Якщо ця умова задовольняється, то на відміну від вищеописаної методики послідовності і доповнюються іншим числом нульових відліків. В результаті еквівалентна періодична послідовність матиме в кінці періодів нулів. Ясно, що ці відмінності ніяк не спотворюють бажаного результату. Можливість довільного вибору істотна, оскільки практичні алгоритми обчислення ДПФ при різних мають неоднакову ефективність. Так, наприклад, для деяких алгоритмів необхідно, щоб дорівнювало ступеня 2. У цьому випадку в якості доводиться вибирати число, рівне ступеню 2 і не менше ніж.