Підставляючи координати точки C (6; 5) в цільову функцію, отримуємо рішення задачі:
.

1.5. опуклі безлічі
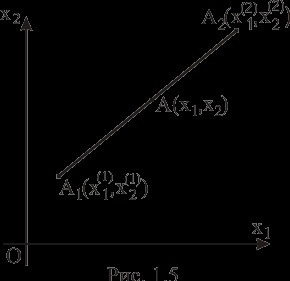
колінеарні, то, де або
, , .
З огляду на, що в (5.12) координати точки A є сумами однойменних координат точок і, помноженим відповідно на,, остаточно отримуємо
Визначення 1.10.ТочкаAявляется опуклою лінійною комбінацією крапок і, якщо для неї виконуються умови (1.13).
Визначення 1.11.В загальному випадку, точкаAявляется опуклою лінійною комбінацією крапок, якщо для неї виконуються умови
Визначення 1.12.Множество називається опуклим, якщо воно містить опуклу лінійну комбінацію будь-яких своїх точок.
Геометрично це означає, що якщо дві точки належать множині, то і відрізок, що з'єднує ці точки, належить цій безлічі.
Прикладами опуклих множин служать відрізок, напівплощина, багатокутник, коло, полупространство, куб і ін.
Визначення 1.13.Точка безлічі називається граничної, якщо будь-яка околиця даної точки містить як точки, що належать безлічі, так і точки, які не належать безлічі.
Визначення 1.14.Множество називається замкнутим, якщо воно містить всі свої граничні точки.
Визначення 1.15.Множество називається обмеженим, якщо таке, що куля радіусомRс центром в будь-якій точці даного безлічі повністю містить це безліч.
Визначення 1.16.Угловой точкою опуклого безлічі називається точка, яка не є опуклою лінійною комбінацією будь-яких різних точок цієї множини.
Безліч може мати будь-яке число кутових точок: одну (рис. 1.6, а), дві (рис. 1.6, б), три (рис. 1.6, в) і т.д. а також нескінченне число кутових точок (рис. 1.6, г).
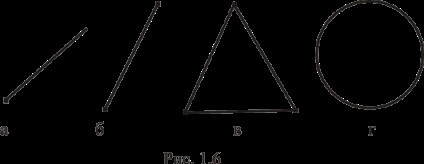
Безліч може і не мати кутових точок, наприклад пряма, напівплощина і т.д.
Визначення 1.17.Многогранніком називається опукле, замкнутий, обмежений безліч, що має кінцеве число кутових точок.
1.6. Властивості рішень задач
Наведені нижче теореми 1.2-1.5 визначають властивості допустимого безлічі рішень і цільової функції на множині допустимих планів.
Теорема 1.2. Безліч допустимих планів задачі (1.15), (1.16) є опуклим безліччю.
Теорема 1.3. Цільова функція задачі (1.15), (1.16) досягає екстремуму в кутовій точці безлічі допустимих планів. Якщо цільова функція досягає екстремуму в декількох кутових точках, то вона досягає екстремуму в будь-який опуклою лінійної комбінації цих точок.
,..., - це вектори умов, тоді система обмежень (1.16) у векторній запису має вигляд:
Теорема 1.4. Якщо система векторів умов лінійно незалежна і така, що
,
де, то - кутова точка безлічі рішень системи обмежень.
Теорема 1.5. Якщо - кутова точка безлічі рішень системи обмежень, то вектори умов, що відповідають позитивним координатами, є лінійно незалежними.
Визначення 1.18.Опорним планом (рішенням) завдання лінійного програмування називається допустимий план, для якого вектори умов, що відповідають його позитивним координатами, лінійно незалежні.
З теорем 1.4 і 1.5 слід, що кутові точки безлічі рішень системи обмежень є опорними планами.
Визначення 1.19.Еслі відмінних від нуля координат опорного планаm, то план називається невироджених, якщо меньшеm- виродженим.
Визначення 1.20.Базісом опорного плану називається базис системи векторів умов, до складу якого входять вектори, відповідні відмінним від нуля координат опорного плану.
З наведених вище теорем 1.2 - 1.5 слід, що оптимальне рішення задачі лінійного програмування (1.15), (1.16) потрібно шукати серед кутових точок безлічі допустимих планів. У зв'язку з цим виникають наступні питання:
- як знайти початковий план?
- як перейти від початкового опорного плану до нового (від однієї кутової точки багатогранника рішень до іншої)?
- як оцінити зміна цільової функції при переході від одного опорного плану до іншого?
- як визначити закінчення процесу перебору кутових точок: або тому, що знайдено оптимальне рішення, або тому, що таке рішення не існує, тобто які умови оптимальності опорного плану?
Відповіді на ці запитання було надано в наступному розділі 1.7.
1.7. Побудова опорних планів
Процес побудови початкового опорного плану, подальшого переходу до нового (краще) опорного плану розглянемо на прикладі задачі ЛП з п'ятьма змінними і трьома рівняннями в системі обмежень. При цьому на першому етапі будемо вважати, що в кожне рівняння системи обмежень і тільки в нього входить змінна з коефіцієнтом.
1.7.1.Построеніе початкового опорного плану
Будемо розглядати задачу
Система рівнянь (1.19) містить три одиничних вектора
, , .
Вони утворюють базис в системі векторів,,,,.
Відповідно до загальної схемою рішення невизначених СЛАР оголошуємо змінні,, базисними, а, - вільними і вважаємо,. Тоді СЛАР (1.19) прийме наступний вигляд:
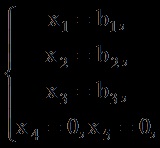
а рішенням СЛАР буде вектор. Отриманий план буде допустимим планом, так як його позитивним координатами відповідають лінійно незалежні вектори,, і
.
Побудований початковий опорний план доставляє цільової функції значення
.
Розглянемо конкретний приклад
Приклад 1.4. Вирішити задачу ЛП.
1. Вибір початкового опорного плану
Безліч допустимих планів задачі визначається системою лінійних рівнянь (1.21). Цю систему можна переписати у векторній формі