2. ЛІНІЙНІ ГРУПОВІ КОДИ
Лінійним називається код, в якому перевірочні символи являють собою лінійні комбінації інформаційних. Груповим називається код, який утворює алгебраїчну групу по відношенню операції додавання по модулю два.
Властивість лінійного коду: сума (різниця) кодових векторів лінійного коду дає вектор, що належить цим кодом. Властивість групового коду: мінімальне кодове відстань між кодовими векторами одно мінімальній вазі ненульових векторів. Вага кодового вектора дорівнює числу одиниць в кодової комбінації.
Групові коди зручно задавати за допомогою матриць, розмірність яких визначається параметрами k і n. Число рядків одно k, а число стовпців одно n = k + m.
Коди, породжувані цими матрицями, називаються (n, k) -код, а відповідні їм матриці породжують (утворюють, що виробляють). Породжує матриця G складається з інформаційної Ikk і перевірочної Rkm матриць. Вона є стислим описом лінійного коду і може бути представлена в канонічній (типової) форми
В якості інформаційної матриці зручно використовувати одиничну матрицю, ранг якої визначається кількістю інформаційних розрядів
Рядки одиничної матриці являють собою лінійно-незалежні-сімие комбінації (базисні вектора), т. Е. Їх по парне підсумовування по модулю два не приводить до нульової рядку.
Рядки породжує матриці являють собою перші k комбінацій коригуючого коду, а інші кодові комбінації можуть бути отримані в результаті підсумовування за модулем два всіляких поєднань цих рядків.
Стовпці додаткової матріциRkm визначають правила формування перевірок. Число одиниць в кожному рядку додаткової матриці повинна задовольняти умові r1 ³ d0 -1, але число одиниць визначає число суматорів за модулем 2 в шифраторі і дешифраторі, і чим їх більше, тим складніше апаратура.
Виробляє матриця коду G (7,4) може мати вигляд
Процес кодування полягає у взаємно - однозначним дотриманням k-розрядних інформаційних слів - I і n-розрядних кодових слів - з
Наприклад: інформаційномуслову I = [1 0 1 0] відповідає наступне кодове слово
При цьому, інформаційна частина залишається без змін, а коригувальні розряди визначаються шляхом підсумовування по модулю два тих рядків перевірочної матриці, номера яких співпадають з номерами розрядів, що містять одиницю в інформаційній частині коду.
Процес декодування полягає у визначенні відповідності прийнятого кодового слова, переданому інформаційному. Це здійснюється за допомогою перевірочної матриці H (n, k).
де Rmk T -транспонірованная перевірочна матриця (поміняти рядки на стовпці); Imm - одинична матриця.
Для (7, 4) - коду перевірочна матриця має вигляд
Між G (n, k) і H (n, k) існує однозначна зв'язок, т. К. Вони визначаються відповідно до правил перевірки, при цьому для будь-якого кодового слова має виконуватися рівність cH T = 0.
Рядки перевірочної матриці визначають правила формування перевірок. Для (7, 4)-коду
Отриманий синдром порівнюємо зі стовпцями матриці і визначаємо розряд, в якому сталася помилка, номер стовпця дорівнює номеру помилкового розряду. Для виправлення помилки помилковий біт необхідно проинвертировать.
Приклад 1. Побудувати груповий код здатний передавати 16 символів первинного алфавіту з виправленням одиночної помилки. Показати процес кодування, декодування і виправлення помилки для переданого інформаційного слова 1001.
1. Побудуємо виробляє матрицю G (n, k).
Якщо обсяг коду N = 2 k = 16, то кількість інформаційних розрядів к = 4. Мінімальна кодова відстань для виправлення одиночної помилки d0 = 2s + 1 = 3. За заданій довжині інформаційного слова, використовуючи співвідношення:
n = k + m, 2 n ³ (n + 1) 2 k і 2 m ³ n + 1
обчислимо основні параметри коду n і m.
Звідки n = 7, т. Е. Необхідно побудувати (7, 4) -код.
В якості інформаційної матриці Ik (7, 4) - вибираємо одиничну матрицю (4'4), а в якості перевірочної матриці Rkm (7, 4) - вибираємо матрицю (4'3), кожен рядок якої містить число одиниць більше або дорівнює двом (r1 £ d0 -1).
Таким чином, в якості виробляє можна прийняти матрицю
.
Інформація про роботу «Коригувальні коди»
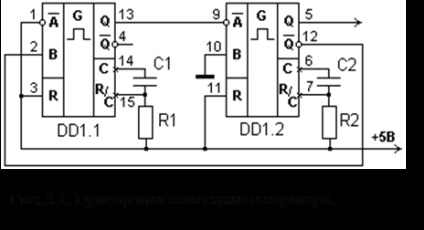
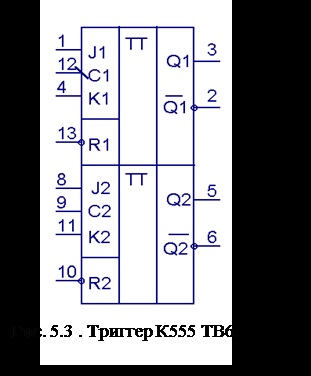
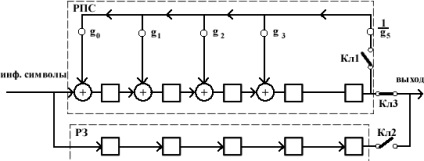
зворотного зв'язку з цим не через n-k зрушень, а відразу з першого такту. Це дозволяє усунути розрив між інформаційними і перевірочними символами. Мал. 1.1. Кодує пристрій для циклічного коду на основі (n-k) - розрядного регістра зсуву. У початковому стані ключ К1 знаходиться в положенні 1, а ключ К2 замкнутий. Інформаційні символи одночасно надходять як.
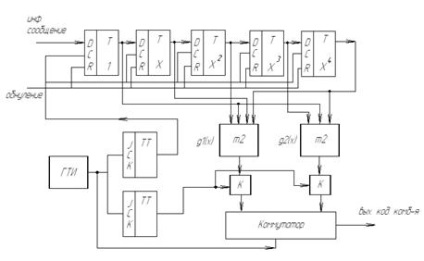
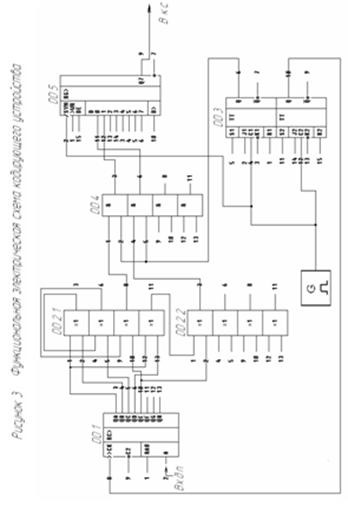
за методом максимальної правдоподібності, тобто оптимальним чином. Оптимальне декодування передбачає, що декодер буде виправляти більше число помилок, ніж порогове значення. 2. Розробка кодує пристрої для формування згортальної коди 2.1 Розробка структурної схеми кодує пристрої для формування згортальної коди Основою для побудови структурної.
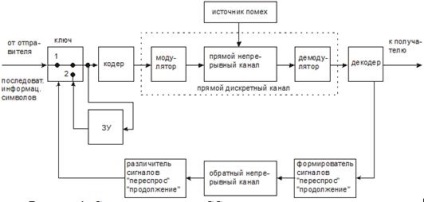
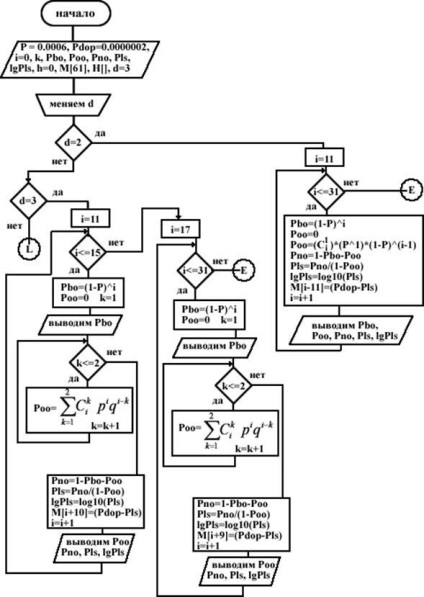
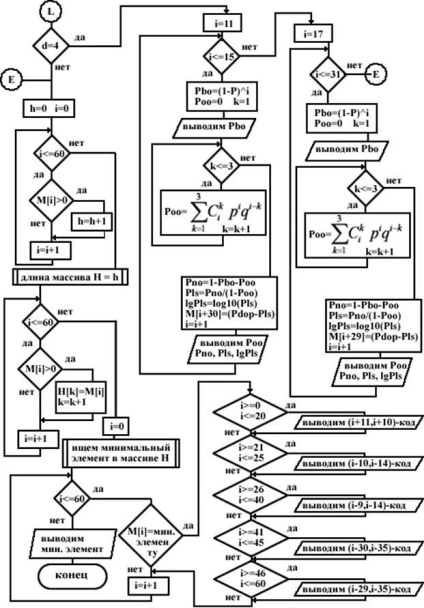
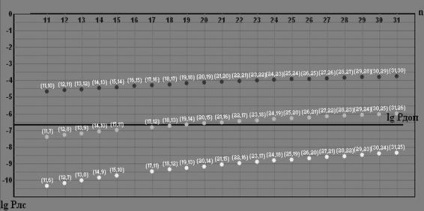
з ЗУ передавача чергової порції інформації, наступна порція не передається до тих пір, поки не буде отримана відповідь з цієї порції. Порядок розрахунку РЛС і приклад розрахунку РЛС для циклічного (n, k)-коду Хеммінга, що забезпечує мінімум різниці Рдоп - РЛС (n, k): Зробимо розрахунок для (18,13)-коду з d = 3. Для цього введемо позначення: · Pбо - ймовірність появи на виході ДСК комбінації.
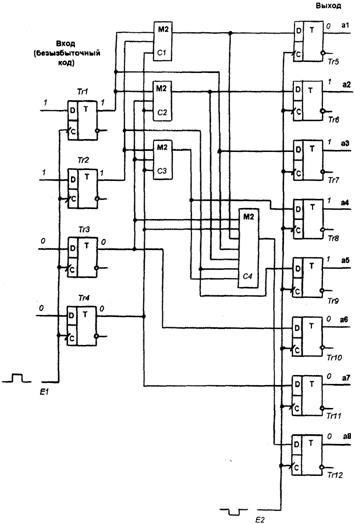
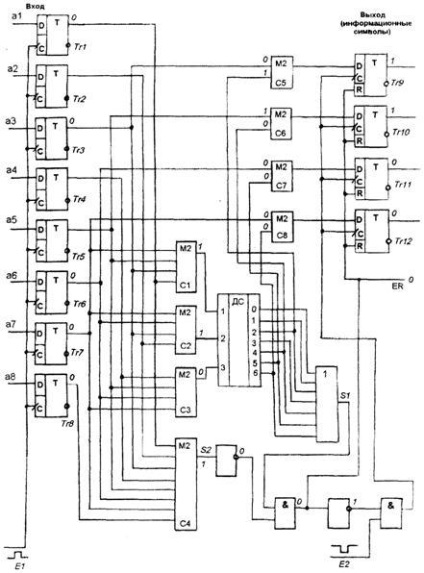
ще одне: Ми отримали остаточні правила побудови коду, здатного виправляти всі одиночні і виявляти подвійні помилки: Використовуючи правила побудови коригуючого коду (*), побудуємо таблицю дозволених комбінацій групового коду обсягом 9 слів, здатного виправляти всі одиночні і виявляти подвійні помилки. У колонку «безизбиточний код» записуємо дев'ять (за завданням Q = 9).