
Логарифмічний папір з числовими координатами від (1; 1) до (100; 100)
Логарифмічний папір - різновид масштабно-координатної паперу. на якій координатна сітка побудована в логарифмічному масштабі. Зазвичай виготовляється друкарським способом. Також використовується напівлогарифмічний папір, на якій уздовж однієї осі відкладена рівномірна шкала, по інший - логарифмічна.
Логарифмічна і напівлогарифмічний паперу застосовуються для побудови графіків функцій. які в логарифмічному масштабі приймають більш простий вигляд (в деяких випадках - пряма). Вони зручні для графічного представлення даних, що змінюються в дуже великому діапазоні значень (на кілька порядків). Природно, аргумент і (або) функція. відкладені за логарифмічною шкалою, повинні приймати тільки позитивні значення.
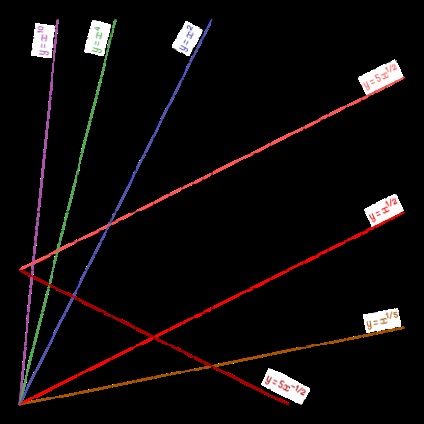
Графіки статечних функцій в логарифмічному масштабі
На логарифмічною папері вид прямих мають графіки статечних функцій виду y = a x b>. оскільки шляхом логарифмування ступенева залежність приводиться до лінійної: l g y = l g a + b l g x \, y = \ mathrm \, a + b \, \ mathrm \, x>. Нахил прямої (кутовий коефіцієнт) визначається показником ступеня b. При b> 0 ця функція зростаюча, а при b <0 убывающая; при b = 0 прямая горизонтальна, y = a . Точка пересечения прямой с осью ординат определяется коэффициентом a. В частности, при a = 1 графики y = x b> являють собою прямі, що проходять через початок координат: l g y = b l g x \, y = b \, \ mathrm \, x>.
На полулогарифмической папері з логарифмічною шкалою по осі абсцис вид прямих мають графіки логарифмічних функцій y = log b (a x) (ax)>. Кутовий коефіцієнт прямої визначається підставою логарифма b. функція зростає в разі b> 1 і спадає при 0 .
На полулогарифмической папері з логарифмічною шкалою по осі ординат вид прямих мають графіки показових функцій y = a b x>. Експоненціальна залежність зводиться до лінійної шляхом логарифмування: l g y = l g a + x l g b \, y = \ mathrm \, a + x \, \ mathrm \, b>. Кутовий коефіцієнт прямої визначається підставою ступеня b. функція зростає в разі b> 1 і спадає при 0 .