Магічні квадрати і паліндроми від Георгія Александрова
Шановний Євгене!
Посилаю Вам метод побудови магічного квадрата непарного порядку, який я сам розробив. Широко відомі способи БАШЕЄВ, Лубер та інших. Але моє рішення, мабуть, найпростіше. Це добре видно з доданих ілюстрацій. Спершу виділяється ромбовидное ядро (жовтий колір), який заповнюється регулярним способом непарних рядом чисел. Потім методом відображення виділяється більш округле ядро шляхом відображення ступеневої трикутника щодо двох сторін рамки. Це ядро також регулярно заповнюється парних поруч чисел. Далі здійснюється просте перенесення трикутних елементів по горизонталі, вертикалі і діагоналі. У мене аж дух перехопило, коли отримав таке!
Навіть сумнів виникло: може, не я першовідкривач? Але як не старався знайти в літературі щось схоже, - нічого не виявив.
Якщо читачам "Кавуна" вдасться знайти першоджерело, то благаю повідомити на renuar911 [dog] yandex.ru
З повагою, Георгій Александров.
Метод побудови магічного квадрата непарного порядку.
Метод розробив Георгій Александров
Магічний квадрат порядку подвійний парності.
Магічна сума у всіх спрощених квадратах дорівнює 2,5 n. тобто в наших випадках 15
З метою більшої наочності останнє рішення краще уявити графічно:
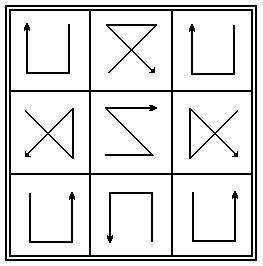
Для того, щоб побудувати наступний спрощений магічний квадрат, тобто близько n = 10, досить по периметру додати пояс умовних значків:
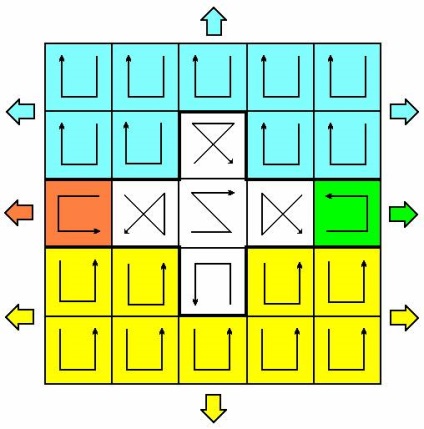
Виділений горизонтальний коридор, а також дві великі зафарбовані області, необмежено простягаються в сторони, дозволяючи тим самим створювати більші матриці порядку 4k +2. Кожна кольорова стрілка підказує, що в даному напрямку ніякі інші значки включати не потрібно.
Отже, ми звели задачу до побудови магічного квадрата непарного порядку n / 2. в якому кожна клітинка 2 х 2 має виявлену тільки що послідовність розстановки чисел.
Так само, як і в випадку магічного квадрата непарного порядку, виділяємо два ядра: парне і непарне, зберігши при перенесенні осередків умовні значки. Далі записуємо простий натуральний ряд чисел, послідовно переходячи від непарного ядра до парному і назад. На наступному малюнку показана початкова стадія заповнення осередків.
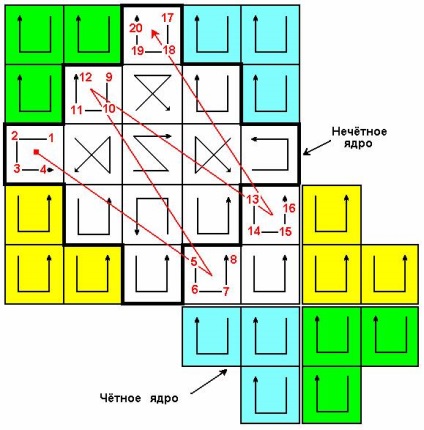
Якщо все числа грамотно розставити, то отримаємо наступне: