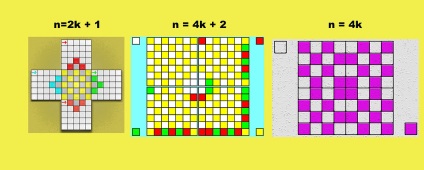
метод терас
Описано Ю. В. Чебраковим в «Теорії магічних матриць».
Для заданого непарного n накреслив квадратну таблицю розміром n на n. Влаштуємо до цієї таблиці з усіх чотирьох сторін тераси (пірамідки). В результаті отримаємо ступінчасту симетричну фігуру.
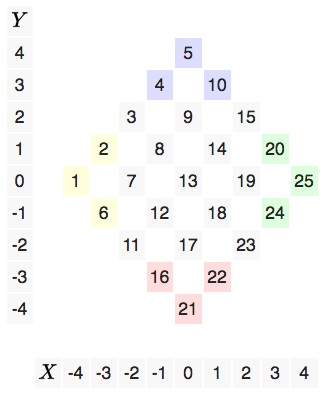
Починаючи з лівої вершини ступінчастою фігури, заповнимо її діагональні ряди послідовними натуральними числами від 1 до N 2.
Після цього для отримання класичної матриці N-го порядку числа, що знаходяться в терасах, поставимо на ті місця таблиці розміром N x N. в яких вони опинилися б, якщо переміщати їх разом з терасами до того моменту, поки підстави терас НЕ долучаться до протилежної сторони таблиці.
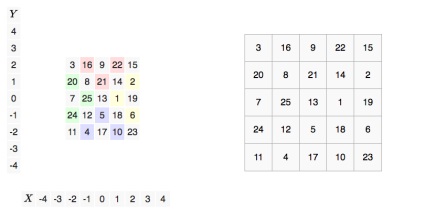
Крім того, даний спосіб є вірним і в тому випадку, якщо магічний квадрат потрібно скласти не з чисел від 1 до N. але і від K до N, де 1 ≤ K 4. Найпростіше конструкція для магічного (i, j) квадрата непарного порядку. Потрібно в клітку з координатами поставити число
1 + ((i - j + (n - 1) / 2) mod n) n + ((i + j + (n + 1) / 2) mod n)
* При виконанні даної операції можливе отримання негативних значень у верхньому правому куті матриці. В даному випадку потрібно скласти n 2 і вийшло негативне число. Однак слід зауважити, що вийшов квадрат буде полумагические.
Ще простіше побудова виконати наступним чином. Береться матриця n x n. Усередині її будується ступінчастий ромб. У ньому осередку зліва вгору по діагоналях заповнюються послідовним поруч непарних чисел. Визначається значення центрального осередку C. Тоді в кутах магічного квадрата значення будуть такими: верхня права клітинка C - 1; нижня ліва комірка C + 1; нижня права комірка C - n; верхня ліва комірка C + n.
Заповнення порожніх клітинок в східчастих кутових трикутниках ведеться з дотриманням простих правил:
1) по рядках числа зліва направо поступово збільшуються на n + 1;
2) за стовпцями зверху вниз числа збільшуються з кроком n - 1.
Також розроблені алгоритми побудови пандіагональних квадратів, і ідеальних магічних квадратів 9x9. Ці результати дозволяють будувати ідеальні магічні квадрати порядків n = 9 (2k + 1) для k = 0,1,2,3. . Існують також загальні методи компонування ідеальних магічних квадратів непарного порядку n> 3. Розроблено методи побудови ідеальних магічних квадратів порядку n = 8k, k = 1,2,3 ... і досконалих магічних квадратів. Пандіагональних і ідеальні квадрати парному-непарного порядку вдається скомпонувати лише в тому випадку, якщо вони нетрадиційні. Проте, можна знаходити майже пандіагональних квадрати. Знайдена особлива група ідеально-скоєних магічних квадратів (традиційних і нетрадиційних).
Приклади більш складних квадратів
Методично суворо відпрацьовані магічні квадрати непарного порядку і порядку подвійний парності. Формалізація квадратів порядку одинарної парності набагато важче, що ілюструють такі схеми:
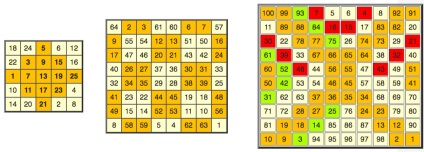
Існують кілька десятків інших методів побудови магічних квадратів
шаховий підхід
Відомо, що шахи, як і магічні квадрати, з'явилися десятки століть тому в Індії. Тому невипадково виникла ідея шахового підходу до побудови магічних квадратів. Вперше цю думку висловив Ейлер. Він спробував отримати повний магічний квадрат безперервним обходом коня. Однак, це зробити йому не вдалося, оскільки в головних діагоналях суми чисел відрізнялися від магічної константи. Проте шахова розбивка дозволяє створювати будь-магічний квадрат. Цифри заповнюються регулярно і через підрядник з урахуванням кольору осередків.