де # 956; 0 - магнетон Бора, служить одиницею виміру атомних і молекулярних магнітних моментів і чисельно дорівнює
Так як заряд електрона негативний, то орбітальний магнітний момент електрона спрямований в бік, протилежний напрямку вектора його орбітального моменту кількості руху
Якщо атом перебуває в зовнішньому магнітному полі, то тому електрон має орбітальним магнітним моментом, вектори магнітного моменту
l і моменту кількості руху
l займуть по відношенню до магнітного поля H певне положення в просторі.
Згідно з квантовою механікою проекції вектора
l на якесь заданий напрямок, в тому числі і напрямок магнітного поля, можуть бути тільки рівними
) = H / (2π) · l * · Cos (
З (14) і (18) випливає, що енергія взаємодії = # 956; l і # 956; S із зовнішнім магнітним полем
по порядку величини буде # 916; # 917;
Звідси для H = 10 4 е, # 916; # 917;
5 · 10 -5 ев, тобто енергія взаємодії # 956; l і # 956; S з H 4
10 е менше енергії - взаємодії для низько розташованих рівнів.
Існування механічного (спина) і магнітного моментів у електрона і пояснення їх властивостей випливає з релятивістської квантової механіки, з основного її рівняння - рівняння Дірака. Зокрема, зрелятивістської квантової механіки слідують співвідношення (15), (16), (17), справедливість яких, як і існування спина, підтверджується експериментами.
В експериментах зазвичай підтверджується не сам магнітний момент мікросистеми, а його проекція. Згідно (17), скільки ms =
1/2, проекція власного магнітного моменту електрона за абсолютною величиною дорівнює одному магнетону Бора
Часто під власним магнітним моментом електрона на увазі не його значення (15), а значення його проекції (17) і говорять, що електрон має магнітним моментом, рівним по абсолютній величині одному магнетону Бора.
§3. Повний магнітний момент одноелектронного атома
До сих пір ми розглядали поведінку орбітального
S магнітних моментів електрона в зовнішньому магнітному полі в припущенні відсутності взаємодії між ними. Однак, у відсутності зовнішнього магнітного поля між цими моментами існує взаємодія, в результаті якого мають місце взаємодії між орбітальним
s моментами кількості руху електрона (ls - взаємодія). При цьому вектори
s прецессируют щодо вектора повного моменту кількості руху
J чисельно рівного
J орієнтуються певним чином в просторі щодо направлення магнітного поля, що називається "просторовим квантуванням".
§4. Досліди Штерна і Герлаха
На пролітають через неординарне магнітне поле атоми діятиме не тільки момент сил, який прагне повернути їх магнітні моменти в напрямку поля, але буде діяти система, що відхиляє сила, обумовлена неоднаковою напруженістю магнітного поля біля полюсів атомного магнітного диполя.
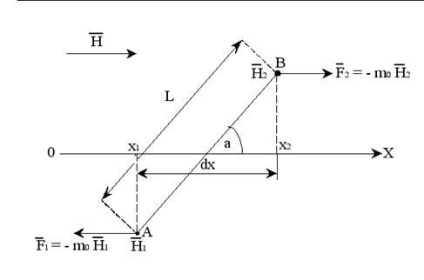
Нехай m0 - величина "магнітного заряду", зосередженого в кожному з полюсів атомного магнітного диполя. H1 і H2 - напруженість магнітного поля в точках A і B. Сила, діюча на диполь з боку поля
в напрямку OX, дорівнює FX = F2 - F1 = m0 (H2 - H1) = m0 (dH / dx) dx.
# 956; = M0 L - магнітний момент диполя.
Залежно від орієнтації магнітного моменту (кут # 945;), диполь буде зміщується вздовж осі ОХ (тобто уздовж поля) або в бік збільшення напруженості магнітного поля.
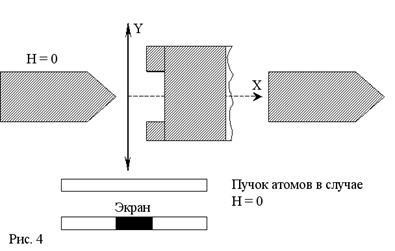
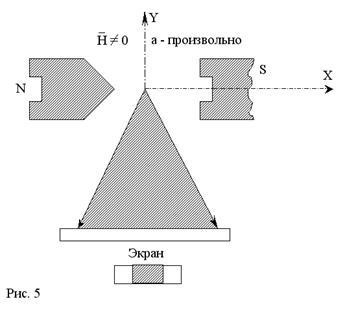
Якщо атоми мають магнітними моментами, які можуть довільно орієнтуватися щодо поля, то вузький первісний пучок атомів, що летить уздовж осі OY, перетинаючи неоднорідне магнітне поле, спрямоване вздовж осі OX, розтягнеться в широку (в напрямку поля) смугу, відповідно до довільними значеннями cos # 945; в межах
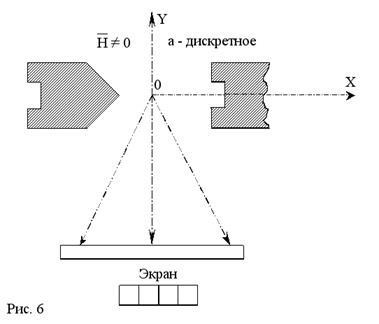
Якщо магнітні моменти атомів можуть орієнтуватися щодо направлення поля тільки цілком певним чином, тобто cos # 945; може приймати тільки цілком певні дискретні значення, то відповідно до цього первинний пучок повинен розщепнутися на ряд компонент. Як випливає з висновку співвідношення (30).
Досліди можуть довести не тільки існування магнітного моменту у атома, але і перевірити достовірність висновків теорії просторового квантування.
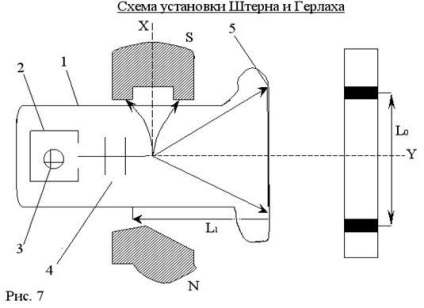
У відкачати до глибокого вакууму посудині 1 поміщена маленька піч 2, в якій знаходиться шматочок срібла 3. При нагріванні печі срібло випаровується, атоми Ag вилітають з печі у всіх можливих напрямках з тепловими швидкостями (
кілька сотень м / с). Кілька щілин 4 виділяють вузький пучок атомів срібла, що летить уздовж осі Y. Атомний пучок пролітає через область неоднорідного магнітного поля, спрямованого уздовж осі X. На пластині 5, пучок конденсується на ній. Атомний пучок розщеплюється, що підтверджує справедливість теорії просторового квантування, доведено наявність у атомів магнітного моменту.
Повний магнітний момент атома # 956; J = # 956; 0 gj *,
де квантове число mJ = j, j - 1, ..., - j.
Всі атоми срібла знаходяться в основному стані 2 S4. орбітальним l = 0, спіном S = ½, внутрішнім j = ½, множник Ланде
g = 1 + (j (j + 1) + s (s + 1) - l (l + 1)) / 2j (j + 1)) = 2
Магнітне квантове число mJ при j = ½ приймає тільки два значення i + ½ і - ½
Отже, можливі тільки дві орієнтації магнітного моменту атома срібла в S - стані щодо поля H.
З боку поля H, згідно (31) буде діяти сила або
dx). Тому одні атоми зміщуються в бік зростання поля, інші - в бік зменшення напруженості
, внаслідок чого пучок розщеплюється на дві компоненти, що підтверджено на досвіді.
Тому в S - стані l = 0, то # 956; l = 0 (# 956; l = (e / 2mC) Pl), отже, магнітний момент атома срібла в основному стані обумовлений власним магнітним моментом електрона, і було визначено в 1952 р
а не # 956; SH = 2 # 956; 0 ms = # 956; 0. що випливає з релятивістського рівняння Шредінгера, рівняння Дірака. Це отримало спеціальну назву - аномального магнітного електрона. Аномальний магнітний момент електрона обумовлений його взаємодією з власним електромагнітним полем.
Є переконливим експериментальним доказом існування магнітного атомного моменту і його просторового квантування.
Якщо світло від джерела розглядати в напрямку перпендикулярному магнітному полю (уздовж осі У), то кожна лінії розщеплена і складається з трьох компонентів:
# 957; 0; # 957; 0 + # 916; # 957 ;; # 957; 0 - # 916; # 957 ;; де # 957; 0 - частота лінії за відсутності магнітного поля;
# 916; # 957; 0 = eH / 4πmC;
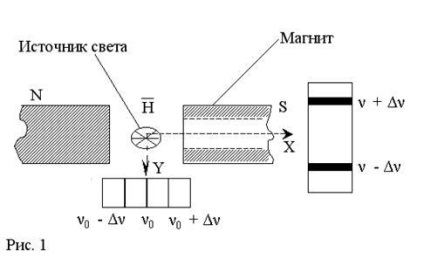
H - напруженість зовнішнього магнітного поля.
Якщо світло розглядати вздовж напрямку магнітного поля
(Уздовж осі Х), то кожна розщепиться тільки на дві компоненти:
За відсутності магнітного поля атом знаходиться в стані з енергією EY. Помістимо його в зовнішнє поле