Побудова багатогранників орігамним методом
Баркалова Вікторія Олександрівна
вчитель математики
ГБОУ ЗОШ № 683
м. Санкт-Петербург
Росія
У цьому майстер-класі буде показано, як будується модуль "Сонобе" і на його основі побудований гексаедр, а також які багатогранники побудували учні різних класів використовуючи цей модуль.

Неоціненну допомогу в виготовленні багатогранників може принести орігамі. Можна виготовити багатогранник будь-якого розміру без всякої викрійки. Потрібно тільки вибрати розмір аркуша паперу.

Для того, щоб побудувати такий гексаедр, необхідно зробити 6 однакових модулів. Модель цікавіше буде, якщо прорахувати кольору модулів.

Побудова модуля "Сонобе". Зігнути квадратний аркуш паперу навпіл і чітко виділити його осьову лінію.

Розгорнути зігнутий лист і загорнути два протилежних кінця до виділеної лінії. Ніяких відхилень не повинно бути.

Один кінець отриманого прямокутника зігнути до протилежної сторони. Виділити лінію згину.

Аналогічно вчинити з протилежним кінцем. Отримаємо паралелограм. У цьому параллелограмме необхідно отримати ще дві лінії згину.
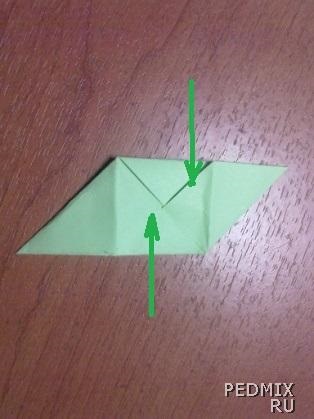
Ось такий модуль повинен вийти. Паралелограм, що має дві кишені для з'єднання з іншими паралелограма. По суті тут 4 кишені, але використовуються тільки два, ті які мають продовження.

Гострий кінець вставляємо в кишеню.

Аналогічно проробляємо з усіх боків.

Бічні стінки зробили. Залишається теж саме проробити знизу і зверху.

Отримаємо гексаедр без клею.

З цього модуля можна сконструювати зірчастий багатогранник.

З 60 модулів вийде інший зірчастий багатогранник!

А ось, що зробили дев'ятикласники за допомогою того ж модуля.


Гексаедр, але з більшої кількості модулів. Робота могла б бути дуже цікавою, якби вона була з різнокольорових модулів.

Багатогранник з 18 модулів.

Чим точніше лінії згину, тим чистіше робота вийде!

Багатогранник з 32 модулів.

Модульне орігамі урізноманітнює ваші уроки геометрії!