Розглянемо основні особливості завдання КТ на прикладі трансмісійної томографії.
Обмежимося завданням на площині - коли просторова структура об'єкта описується функцією двох координат, а її відновлення проводиться за функціональністю (проекцій) від однієї змінної.
Нехай плоский пучок рентгенівських променів з інтенсивністю / 0 проходить через об'єкт (див. Рис. 1) в площині (X, Y). нехай 5
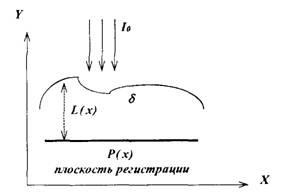
Мал. 1. Схема трансмісійної томографії
дження через яка поглинає середу. Припустимо, що коефіцієнт загасання в об'єкті постійний: 8 (у) = з> "= const.
Тоді найпростішої завданням томографії (зворотної завданням) є отримання форми об'єкта і значення 8д по функції І (х).
При проходженні малого шару поглинаючого середовища Ду зміна інтенсивності випромінювання пропорційно товщині цього шару і коефіцієнт загасання:
Якщо проінтегрувати (1) по вертикальній координаті уздовж кожного з променів, складових поперечний переріз пучка, отримаємо зображення об'єкта в площині реєстрації:
Вираз (2) становить основу трансмісійної томографії: за відомою функції Р (х) необхідно отримати функцію д (у) # 9632; При S (y) = S0 = const інтегрування (2) дає.
Навіть в цьому простому випадку рішення задачі можливо тільки за певних умов: для отримання форми об'єкта (функції L (x)) необхідно знати значення коефіцієнта загасання, або, навпаки, для знаходження коефіцієнта загасання необхідно знати форму об'єкта. Крім того, в даній постановці завдання існує нескінченне число об'єктів, які в площині реєстрації дають однакову проекцію Р (х). Дійсно, якщо нижня межа об'єкта не плоска, то кожної функції товщини Ь (х) відповідає нескінченне число об'єктів різної форми. Якщо опромінювати об'єкт під іншим кутом, то проекція в площині реєстрації буде інший, однак проблеми з неоднозначністю відновлення об'єкта залишаться. Таким чином, відновлення об'єкта вимагає від нас інформації про проекціях, отриманих під різними кутами. При цьому ми повинні заздалегідь припустити, що об'єкт є тілом з постійним коефіцієнтом загасання всередині нього. Або нам потрібно значно більше число зображень об'єкта. Отже, для розв'язання оберненої задачі нам необхідна апріорна інформація (a priori - латиною - «з попереднього»). Таку властивість має абсолютну більшість завдань томографії. В математиці ці завдання називають некоректними [17]. Їх основні властивості - неоднозначність рішення, а також той факт, що нескінченно малі погрішності в початкових даних можуть привести до кінцевих погрішностей в результаті обчислень [7, 11]. Простий приклад: малі зміни коефіцієнта загасання S (v) у натуральному вираженні (2) за рахунок інтегрування по променю L (\) можуть призводити до значних змін зображення в площині реєстрації Р (х).
Розвиток методів розв'язку обернених задач являє собою великий розділ сучасної математичної фізики та дискретної математики. У практичних додатках такі теоретичні дослідження дозволяють створювати оптимальні схеми сканування для різних видів томографії [6, 14]
Крім розглянутої нами трансмісійної томографії широкого поширення набула емісійна томографія. Вона використовується в ядерній медицині, оптичної і радіотеплолока- ції (радіометрії) [5, 14]. Відмінність емісійної томографії полягає в тому, що вона являє собою типовий приклад пасивних вимірювань - для відновлення інформації про об'єкт використовується його власне випромінювання (рентгенівське, оптичне, СВЧ) [5, 14]. Наприклад, в ядерній медицині завдання полягає в тому, щоб знайти просторовий розподіл радіоактивного препарату усередині тіла по інтенсивності випромінювання, що вимірюється поза тілом. Як і всі завдання пасивного хвильового зондування, таке завдання виявляється складніше розглянутої вище, і в плоскому випадку замість виразу (2) зображення в площині реєстрації матиме вигляд:
де а - поточна координата джерела випромінювання, F
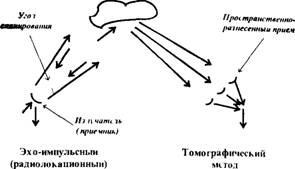
Рис 2 Відмінність луна-імпульсного від томографічного методу зондування
Акустична томографія (АТ) заснована на розв'язанні обернених задач розсіяння і рефракції.
Відмінність акустичної томографії від традиційного луна-імпульсного (радіолокаційного) методу ультразвукового зондування схематично показано на рис. 2.
В обох випадках передбачається кутовий сканування об'єкта, однак для відновлення його структури методом томографії необхідний просторово-рознесений прийом акустичних сигналів. Найчастіше в АТ використовується наближення геометричної оптики (променеве наближення) При цьому джерелом інформації про середовище є не коефіцієнт загасання, а швидкість поширення звуку. Зворотні задачі розсіювання і рефракції з фізичної точки зору відрізняються лише характером неоднорідності і використовуваними приближениями (рис. 3).
Неоднорідність середовища при поширенні хвилі будь-якої природи вздовж напрямку # Один тисяча сто сорок одна; визначається зміною в просторі
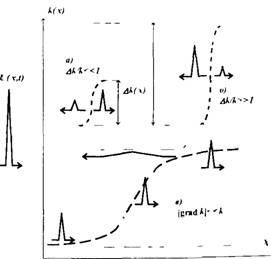
Рис и Основні варіанти розсіювання хвиль в неоднорідному середовищі
де з - циклічна частота, а з (л) - швидкість поширення хвилі. Якщо розміри неоднорідності можна порівняти з довжиною хвилі, то виникає відбита хвиля, амплітуда якої визначається стрибком швидкості і, відповідно, хвильового числа ТАК (г) (верхня частина рис. 3). За умови А к / к «1 енергія прошед-
шей через неоднорідність хвилі практично не зменшується, і при імпульсному зондуванні просторове положення кожної наступної неоднорідності реєструється в слабкому відбитому сигналі в залежності від часу приходу відбитої хвилі в приймач. Таке наближення називається в теорії хвиль наближенням Борна, або одноразового розсіяння [2, 4, 8]. При ехоімпульсного методі зондування в більшості випадків використовується саме це наближення. У протилежному випадку (ДА '/ к »1) хвиля не поширюється в глиб досліджуваного об'єкта і завданням хвильового зондування може бути отримання інформації про форму його кордонів, а не внутрішньою структурою. Дозвіл зондирующих, і, зокрема, ультразвукових пристроїв, збільшується з частотою зі. При цьому для ультразвукових хвиль зі збільшенням частоти збільшується і коефіцієнт загасання 8 до зі '[13], що принципово обмежує просторовий діапазон роботи ультразвукових пристроїв.
У разі плавно-неоднорідного середовища, коли розміри неоднорідності значно перевищують довжину хвилі ((gradk ( «к. См.
Мал. 3), відбитий сигнал може практично відсутні, і для розв'язку обернених задач використовуються принципи рефракційної томографії. У таких завданнях інтегрується фаза хвильових сигналів уздовж променів (траєкторій) поширення хвилі. Промені при цьому є криві, форма яких залежить від швидкості (коефіцієнта заломлення) середовища. Цей коефіцієнт заломлення і є шуканої величиною, просторовий розподіл якої необхідно відновити. Вихідними даними в таких завданнях є тимчасові затримки (фаза) хвильових сигналів, що розповсюджуються вздовж різних променів, або кути приходу променів в різні точки простору. Методи рефракційної томографії отримали широке поширення в сейсмології (для дослідження земної кори), фізики атмосфери (для відновлення висотних атмосферних показників при її просвічуванні в оптичному або радіодіапазоні), океанології (для відновлення профілів щільності, солоності, температури в глибині Світового океану за умовами поширення звукових хвиль) [3, 15, 19, 21, 22].
Розглянемо два основних теоретичних підходи до вирішення зворотних хвильових задач.