Ось вже воістину ніколи не здогадатися, що може знайти застосування в житті. Здавалося б, судоку - просто забавна головоломка. А ось адже і її використовували для алгоритму кодування зображень!
Ультрасучасний алгоритм кодування зображень використовує новий тип матриці, створений на основі головоломки судоку.
Числова головоломка судоку складається з таблички клітин, які повинні бути заповнені цифрами від до.
Є ряд додаткових обмежень. Кожна цифра може з'явитися тільки один раз в кожному стовпці, один раз в кожному рядку і один раз в кожному з дев'яти блоків, що входять до складу таблиці. Рішення головоломки наведено нижче. На початку гри гравцям відомо розташування деякої кількості цифр з цього рішення.
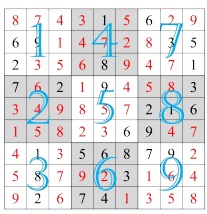
Завдяки судоку виник цілий ряд цікавих для математиків завдань. Раніше в цьому році, наприклад, була вирішена задача про мінімальну кількість ключів для судоку, яке дає до єдине рішення (таких ключів 17).
Тепер Ю Ву з Університету Тафтса в Медфорді і його колеги використовували судоку для вирішення іншого завдання - проблеми кодування зображень перед їх відправкою.
Особливі властивості таблиці судоку привели до появи абсолютно нового типу матриць, який вони використовували для кодування зображень.
По-перше, трохи про матрицях. Матриця - це просто прямокутна таблиця з чисел. Кожен елемент в таблиці однозначно визначається парою чисел: номерами рядка і стовпця, в яких він знаходиться.
Але Ву і його колеги говорять, що можна визначити елементи масиву по-іншому, якщо подумати про нього, як про таблиці судоку. У цьому випадку кожен елемент містить цифру від до, яка задовольняє правилам судоку. Іншими словами, на додаток до номерів рядка і стовпця, кожному елементу відповідає цифра.
Таким чином, у наведеній вище таблиці елементу в першому рядку і першому стовпці також відповідає цифра, елемент пов'язаний з цифрою, елемент - з цифрою і т.д.
До того ж кожен елемент пов'язаний також з блоком, а самі блоки пронумеровані так, як показано на малюнку. Таким чином, елемент пов'язаний з блоком, елемент - з блоком, елемент з блоком, і так далі.
Це дозволяє ідентифікувати кожен елемент інакше. Таким чином, елемент в блоці, що містить цифру - це елемент в звичайних позначеннях; елемент в стовпці, що містить цифру - це елемент в загальноприйняті позначення і елемент в рядку, що містить - це елемент.
В цілому існує шість різних способів подання кожного елемента, згідно Ву і його колегам. Кожна з цих систем позначень може бути використана, і перетворити координати з однієї системи в іншу можна, використовуючи набір простих математичних функцій перетворення.
Ці функції перетворення є ключем до кодування зображень. Почнемо з зображення пікселів. Накласти рішення судоку на нього так, що кожен піксель може тепер бути представлений координатами в новій системі координат.
Тепер, застосовуючи одну з функцій перетворення, міняємо позиції пікселів, змішуючи зображення.
Ву і його колеги відкрили те, як застосовувати коротку послідовність функцій перетворення, яка повністю шифрує зображення. Це корисно, тому що все повністю детерміновано і разом з тим дає, здавалося б, випадковий результат (як показано на верхньому малюнку).
Це еквівалентно типу шифрування, при якому оригінальне рішення судоку є ключем. (Для великих зображень на них просто накладається кілька таблиць судоку).
Ву і його колеги зробили деякі початкові порівняння їх методу і інші алгоритмів кодування зображень. Вони кажуть, що новий алгоритм працює так само швидко або навіть перевершує відомі алгоритми.
Однак Ву і його колеги не роблять ніяких заяв щодо стійкості до злому їх алгоритму, але явно тут потрібно проводити подальші дослідження.
Дивно, скільки судоку може зробити для людства!