Метод зон Френеля.
Обчислення за формулою
є в загальному випадку дуже важке завдання. Однак, як показав Френель, у випадках, що відрізняються симетрією, знаходження амплітуди результуючого коливання може бути здійснено простим алгебраїчним або геометричним підсумовуванням.
Знайдемо в довільній точці М амплітуду сферичної світлової хвилі, що розповсюджується в однорідному середовищі з точкового джерела S.
Згідно з принципом Гюйгенса-Френеля, замінимо дію джерела S дією уявних джерел, розташованих на допоміжній поверхні Ф. є поверхнею фронту хвилі, що йде з S (поверхню сфери з центром S). Френель розбив хвильову поверхню A на кільцеві зони такого розміру, щоб відстані від країв зони до М відрізнялися на λ / 2,
Подібне розбиття фронту хвилі на зони можна виконати, провівши з центром в точці розбиття фронту хвилі на зони можна виконати, провівши з центром в точці М сфери радіусами
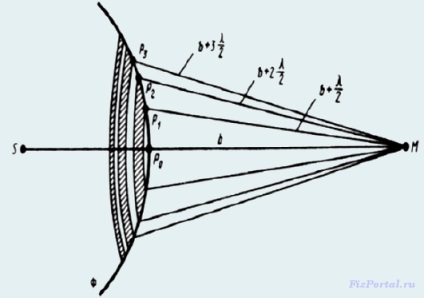
Так як коливання від сусідніх зон проходять до точки М відстані, що відрізняються на λ / 2. то в точку М вони приходять в протилежній фазі і при накладенні ці коливання будуть взаємно послаблювати один одного. Тому амплітуда результуючого світлового коливання в точці М:
де А1. А2. ... А m - амплітуди коливань, порушуваних 1-й. 2-й. ..., m-й зонами.
Для оцінки амплітуд коливань знайдемо площі зон Френеля. Нехай зовнішня межа m-ї зони виділяє на хвильової поверхні сферичний сегмент висоти hm (рис.).
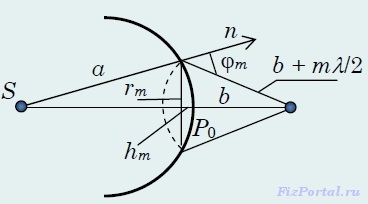
Позначивши радіус цього сегмента через rm. знайдемо, що площа m-ї зони Френеля:
тут σm-1 - площа сферичного сегмента, що виділяється зовнішнім кордоном m - 1-ї зони. З малюнка слід, що
Після елементарних перетворень, враховуючи, що λ <
Площа сферичного сегмента і площа m-ї зони Френеля:
де δσm площа m-ї зони Френеля, яка, як показує останній вираз, не залежить від m. При не дуже великих m площі зон Френеля однакові.
Таким чином, побудова зон Френеля розбиває хвильову поверхню сферичної хвилі на рівні зони.
Знайдемо радіуси зон Френеля
звідки
Згідно з припущенням Френеля, дія окремих зон в точці М тим менше, чим більше кут φm між нормаллю до поверхні зони і напрямком на М. тобто дію зон поступово зменшується від центральної (близько Р0) до периферичних. Крім того інтенсивність випромінювання в напрямку точки М зменшується з ростом m і внаслідок збільшення відстані від зони до точки М. З огляду на обидва ці чинники, можемо записати:
Фази коливань, порушуваних сусідніми зонами, відрізняються на π. Тому амплітуда результуючого коливання в точці М визначається виразом
Останній вираз запишемо у вигляді:
Внаслідок монотонного убування амплітуд зон Френеля зі зростанням номера зони, амплітуда коливання Am від деякої m-ї зони Френеля дорівнює середньому арифметичному від амплітуд примикають до неї зон
тоді
Таким чином, амплітуда результуючих коливань в довільній точці М визначається дією тільки половини центральної зони Френеля. Отже, дія всієї хвильової поверхні на точку М зводиться до дії її малого ділянки, меншого центральної зони.
Якщо на шляху хвилі поставити непрозорий екран з отвором, залишає відкритою тільки першу зону Френеля, амплітуда в точці М дорівнює А1. а інтенсивність в 4 рази більше, ніж при відсутності перешкоди між точками S і M.
Поширення світла від S до M відбувається так, ніби світловий потік поширюється всередині дуже вузького каналу вздовж прямої SM. тобто прямолінійно. Таким чином, принцип Гюйгенса-Френеля дозволяє пояснити прямолінійне поширення світла в однорідному середовищі.
Правомірність розподілу хвильового фронту на зони Френеля підтверджена експериментально. Якщо поставити на шляху світлової хвилі платівку, яка перекривала б все парні або непарні зони Френеля, то інтенсивність світла в точці М різко зростає. При закритих парних зонах Френеля амплітуда в точці М буде дорівнює
Під час експерименту зонная пластинка у багато разів збільшує інтенсивність світла в точці М. діючи подібно збирає лінзі.
Ще більшого ефекту можна досягти, не перекриваючи парні (або непарні) зони Френеля, а змінюючи фазу їх коливань на 180 °. Така пластинка називається фазовою зонного платівкою. У порівнянні з амплітудною зонного платівкою фазова дає додаткове збільшення амплітуди в 2 рази. а інтенсивність світла - в 4 рази.