В теорії реакторів розроблені моделі, що дозволяють врахувати неідеальність потоку. Ці моделі теж є наближеними, однак вони більш точно описують реальний процес, ніж моделі ідеального змішування або витіснення.
Математичні моделі реальних реакторів можуть бути побудовані на основі двох підходів.
Заснований на уявній заміні реального реактора тій чи іншій комбінацією ідеальних апаратів.
При складанні математичного опису прагнуть врахувати всі реальні фізичні явища, що відбуваються в апараті і внести їх в рівняння моделі.
При першому підході математична модель являє собою систему рівнянь, які об'єднують математичні описи декількох ідеальних реактори. Число рівнянь може бути велике, але за структурою вони залишаються такими ж простими, як і рівняння ідеальних моделей.
При другому підході число рівнянь може бути менше, але вони більш складні і отже складні методи їх вирішення.
Більшість виробничих реакторів працює в режимі ча-стичного або локального перемішування реагентів з продуктами реакції, т. Е. Реальний реактор займає деякий проміжний-ве становище між реакторами повного змішання і ідеального витіснення. Такі реактори досить точно описуються так на-зване дифузійної моделлю.
Дифузійна модель. Ця модель математично виражається рівняннями, в яких враховано зміна концентрації не тільки внаслідок хімічного перетворення (як при ідеальному витес-неніі), але і в результаті деякого перемішування реагентів і продуктів реакції за рахунок молекулярної або турбулентної Діффі-зії. Дифузійна модель може бути описана моделлю идеаль-ного витіснення з введенням членів, які враховують відповідаю щее перемішування фаз в реальному апараті.
Радіальне перемішування згладжує температурні і кон-центраціонние поля в горизонтальному (елементарному) шарі і ви-прирівнюються час перебування окремих частинок. Таким чином, ра-діальной перемішування завжди корисно і воно мало впливає на мо-дель реактора. Тому рівняння дифузійної моделі зазвичай записують в однопараметричними вигляді, враховуючи тільки про-дольний перенесення. Для незворотною хімічної реакції п-го по-рядка при сталому (стаціонарному) режимі воно має вигляд
де DL - коефіцієнт поздовжнього перемішування, рівний ефек-тивному коефіцієнту дифузії.
Його зручно представити в безрозміряний-ном вигляді, ввівши нову змінну l-x / L, де L - довжина реактора. тоді x = lL, dx = Ldl. З урахуванням співвідношення
L / ω,
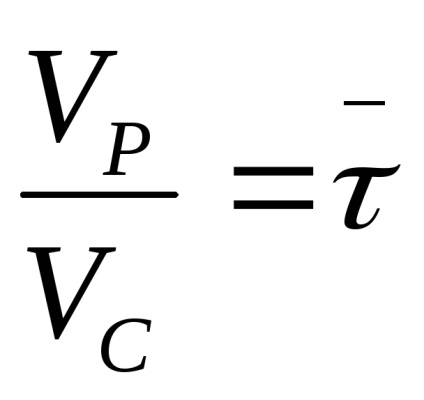
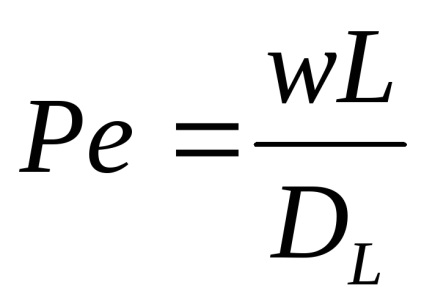
в безрозмірному вигляді рівняння запишеться як
Рівняння вирішується за певними граничними умо-виями і, як правило, з використанням ЕОМ. Воно охоплює весь діапазон реальних реакторів, які працюють без застійних зон і байпасірованія реагентів. Якщо Ре = 0
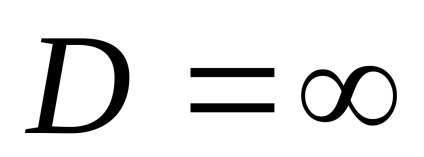
Для реакції першого порядку рішення диференціального рівняння дає сліду-ющий результат:
,
Характер зміни ступеня пре-обертання по висоті реактора при різних числах Пеклі (рис. 1) підтверджує це положення.
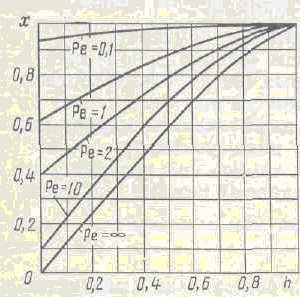
Рис.1. Залежність зміни ступеня перетворення речовини х по висоті ізотермічного реактора-ра при різних значеннях кри-терия Ре
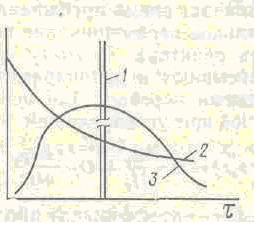
Рис.2. Криві відгуку на імпульсне обурення в реакторах різного типу:
1 - ідеального витіснення; 2 - повного смішить-ня; 3 - довільного режиму
Висновок функцій розподілу часу перебування для реакторів, описуваних однопараметричній дифузійної моделлю заснований на розрахунку концентрації індикатора на виході з реак-тора. Для цього необхідно вирішити диференціальне рівняння дифузійної моделі в нестаціонарному режимі без урахування химиче-ської реакції
У ячеистой моделі реальний апарат мислення розчленовують на N послідовно з'єднаних осередків ідеального змішування.
Сумарний обсяг всіх осередків дорівнює повному обсягу реактора.
Така заміна правомірна з наступних причин: 1) каскад реакторів при N = 1 - одиничний реактор ідеального змішування, а при N = ∞ і нескінченно малих обсягах секцій вироджується в реактор ідеального витіснення.
Таким чином, допомогою моделі каскаду реакторів ідеального змішування можна описати граничні гідродинамічні режими. А в реальному реакторі існує проміжний режим, який можна описати за допомогою моделі каскаду РІС, що складається з N комірок, причому N