Усічення має місце, коли дані вибираються з деякого більшого за обсягом підмножини даних (спостережень), наприклад, в дослідженні доходів розглядаються сім'ї з доходами нижче або вище певного рівня (скажімо, за межу бідності).
Замість усічення вибірок може застосовуватися також їх цензурування. Зокрема, в дослідженнях доходів розглядається вся вибірка, але приймається, що у сімей з доходами вище або нижче певного рівня доходи знаходяться на одному рівні. Наслідком цензурування і усічення вибірок є спотворення значень вибіркових параметрів розподілів, зокрема, їх математичних очікувань і дисперсій. Відповідно висновки, отримані на підставі усічених і цензурованих вибірок, слід дуже обережно поширювати на генеральну сукупність.
Моделі усічених вибірок
Припустимо, усеченное розподіл є частиною неусеченного розподілу, яка знаходиться вище або нижче певного порогового значення.
Щільність безперервної випадкової змінної z. усіченої вище рівня b. визначається відповідно до наступного виразу:
Вираз (10.136) випливає, з формули умовної ймовірності. Справді, умовна ймовірність того, що випадкова величина z прийме деяке значення за умови, що z ò ò /ò Продифференцировав ліву і праву частини виразу (10.137) по z. отримаємо (10.136). У багатьох практичних дослідженнях передбачається, що випадкова величина z розподілена за нормальним законом. У цьому випадку ймовірність того, що z> b визначається відповідно до наступного виразу: де m і s - відповідно математичне очікування і стандартне відхилення випадкової величини z; b = (b -m) / s; Ф (.) - значення стандартної нормальної інтегральної функції розподілу у відповідній точці. Тоді згідно з виразом (10.136), функція щільності усіченого нормального розподілу визначається як: де j (.) - стандартна нормальна функція розподілу. На рис. 10.6 представлені графіки функцій щільності усіченого стандартного нормального розподілу з m = 0 і s = 1 для b = -0,5; 0; 0,5. З графіків, представлених на цьому малюнку слід, що усічення як би "піднімає" функцію щільності на що залишився після усічення ділянці над графіком цієї функції "неусеченного" розподілу. Надалі випадкову змінну з усіченим розподілом будемо називати усіченої випадкової змінної. Зауважимо, що математичне очікування і дисперсія усіченої випадкової змінної визначаються згідно з такими виразами: M [z | z> b] =ò D [z | z> b] =ò Провівши інтегрування в виразах (10.140) - (10.141) з урахуванням того, що функція щільності f (z. Z> b) визначена виразом (10.139), одержимо, що математичне очікування і дисперсія усіченої випадкової змінної z відповідно рівні: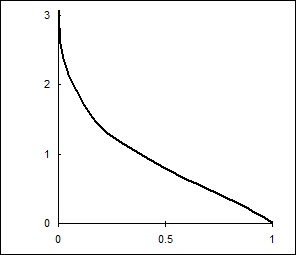
Ріс.10.8. Умовне середнє як функція ступеня усічення.
Припустимо, що залежність деякої випадкової змінної yt. від значень впливають на неї факторів, можна представити таким чином:
де xt - вектор незалежних змінних, що впливають на змінну yt; a - вектор параметрів; et - помилка моделі, щодо якої передбачається, що вона розподілена за стандартним нормальним законом з нульовим математичним очікуванням і постійної дисперсією, et
Мінлива yt. описана вираженням (10.148), розподілена за нормальним законом з математичним очікуванням mt = a ¢ × xt і дисперсією s 2.
Розглянемо розподіл залежною змінною yt за умови, що спостерігаються значення yt перевищують певний поріг b. Згідно зі слів (10.142) одержимо, що умовне математичне очікування yt для моделі (10.148) є нелінійною функцією від ХT і a. і визначається як
M [yt | yt> b] = a ¢ × xt +
Перепишемо вираз (10.149) з використанням функції відмов l (bt) (див. Вираз (10.144)):
З урахуванням виду вираження (10.150) оцінимо величину маржинального ефекту факторів xt для випадку усіченої вибірки:
Оскільки для кожного набору факторів xt виконується співвідношення 0 Зауважимо, що в силу специфіки вираження (10.150) помилка et моделі (10.146), побудованої для усіченої вибірки, має математичне очікування s × l (bt). Дисперсія помилки et в цьому випадку визначається наступним чином: Таким чином, з виразів (10.150) і (10.152) випливає, що оцінки параметрів моделі (10.148), визначені на підставі усіченої вибірки залежною змінною (yt> b або yt