Чисельні методи розв'язання нелінійних рівнянь. Метод хорд.
Метод хорд (метод також відомий як метод січних) один з методів вирішення нелінійних рівнянь і заснований на послідовному звуженні інтервалу, що містить єдиний корінь рівняння. Ітераційний процес виконується до того моменту, поки не буде досягнута задана точність.
На відміну від методу половинного ділення, метод хорд пропонує, що розподіл розглянутого інтервалу буде виконуватися не в його середині, а в точці перетину хорди з віссю абсцис (вісь - Х). Слід зазначити, що під хордою розуміється відрізок, який проведений через точки даної функції по кінцях розглянутого інтервалу. Розглянутий метод забезпечує більш швидке знаходження кореня, ніж метод половинного ділення, при умові завдання однакового розглянутого інтервалу.
Геометрично метод хорд еквівалентний заміні кривої хордою, що проходить через точки і (див. Рис.1.).
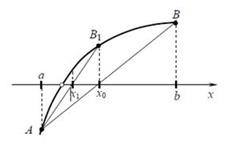
Рис.1. Побудова відрізка (хорди) до функції.
Рівняння прямої (хорди), яка проходить через точки А і В має наступний вигляд:
Дане рівняння є типовим рівнянням для опису прямий ви декартовій системі координат. Нахил кривої задається по ординате і абсциссе за допомогою значень в знаменнику і. відповідно.
Для точки заходу прямий з віссю абсцис записане вище рівняння перепишеться в наступному вигляді:
В якості нового інтервалу для проходження ітераційного процесу вибираємо один з двох або. на кінцях якого функція приймає значення різних знаків. Протилежність знаків значень функції на кінцях відрізка можна визначити багатьма способами. Один з безлічі цих способів - множення значень функції на кінцях відрізка і визначення знака твори шляхом порівняння результату множення з нулем:
Ітераційний процес уточнення кореня закінчується, коли умова близькості двох послідовних наближень стане менше заданої точності, тобто
.
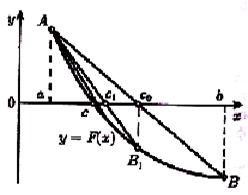
Рис.2. Пояснення до визначення похибки розрахунку.
Слід зазначити, що збіжність методу хорд лінійна, однак більш швидка, ніж збіжність методу половинного ділення.
Алгоритм знаходження кореня нелінійного рівняння за методом хорд
1. Знайти початковий інтервал невизначеності одним з методів відділення коренів. З адать похибка розрахунку (мале позитивне число) і початковий крок ітерації ().
2. Знайти точку перетину хорди з віссю абсцис:
3. Необхідно знайти значення функції в точках. і. Далі необхідно перевірити дві умови:
- якщо виконується умова. то шуканий корінь знаходиться всередині лівого відрізка покласти. ;
- якщо виконується умова. то шуканий корінь знаходиться всередині правого відрізка прийняти. .
В результаті знаходиться новий інтервал невизначеності, на якому знаходиться шуканих корінь рівняння:
4. Перевіряємо наближене значення кореня рівняння на предмет заданої точності, в разі:
- якщо різниця двох послідовних наближень стане менше заданої точності. то ітераційний процес закінчується. Наближене значення кореня визначається за формулою:
- якщо різниця двох послідовних наближень не досягає необхідної точності. то необхідно продовжити ітераційний процес і перейти до п.2 даного алгоритму.
Як приклад, розглянемо рішення нелінійного рівняння методом хорд. Корінь необхідно знайти в даному діапазоні з точністю.
Варіант рішення нелінійного рівняння в програмному комплексі MathCAD.

Результати розрахунків, а саме динаміка зміни наближеного значення кореня, а також похибки розрахунку від кроку ітерації представлені в графічній формі (див. Рис.1).
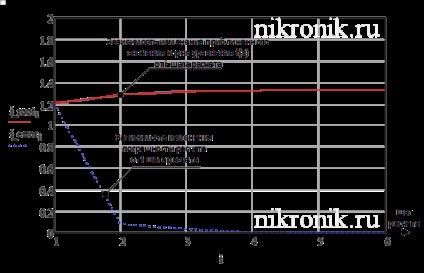
Рис.1. Результати розрахунку за методом хорд
Для забезпечення заданої точності при пошуку рівняння в діапазоні необхідно виконати 6 ітерацій. На останньому кроці ітерації наближене значення кореня нелінійного рівняння буде визначатися значенням:.
Модифікацією даного методу є метод помилкового положення (False Position Method), який відрізняється від методу січних тільки тим, що всякий раз беруться не останні 2 точки, а ті точки, які знаходяться навколо кореня.
Слід зазначити, що в разі якщо від нелінійної функції можна взяти другу похідну алгоритм пошуку може бути спрощений. Припустимо, що друга похідна зберігає постійний знак, і розглянемо два випадки:
З першої умови виходить, що нерухомою стороною відрізка є - сторона a.
З другої умови виходить, що нерухомою стороною відрізка є - сторона b.
У загальному вигляді, для виявлення нерухомого кінця можна записати наступне умова:. де або.
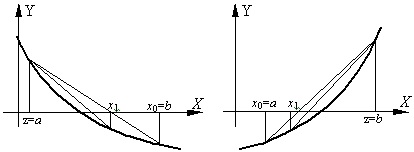
Мал. 3. Приклади спадної або зростаючій функції
Таким чином, в залежності від виду функції виходять два вирази для спрощення пошуку кореня функції:
- якщо функція відповідає першому випадку (див. рис. 3), тоді формула буде мати такий вигляд:
- якщо функція відповідає другому випадку (див. рис. 3), тоді формула буде мати такий вигляд:
Випадок зводиться до розглянутого. якщо рівняння записати у формі:.