Умова задачі:
На сферичної планеті вага тіла на полюсі в 3 рази більше ваги тіла на екваторі. Визначте період обертання цієї планети, якщо її середня щільність 2300 кг / м 3.
Завдання №2.5.9 з «Збірника завдань для підготовки до вступних іспитів з фізики УГНТУ»
\ (P_п = 3P_е \), \ (\ rho = 2300 \) кг / м 3. \ (T -? \)
Рішення завдання:
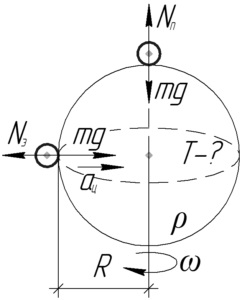
Тіло, що перебуває на екваторі, обертається разом з планетою, описуючи коло радіуса \ (R \) (радіус планети). Другий закон Ньютона для цього тіла запишеться в наступному вигляді:
Тіло на полюсі обертається навколо своєї осі, оскільки вісь планети проходить через центр мас цього тіла. Так як при обертанні планети воно буде описувати коло нульового радіуса, значить на нього не діє доцентровийприскорення. Перший закон Ньютона для цього тіла буде записаний в такому вигляді:
Отримаємо таку систему:
З огляду на (1), маємо:
Так як за умовою \ (P_п = 3P_е \), то поділивши нижню рівність системи на верхнє, отримаємо:
Висловимо прискорення вільного падіння \ (g \) на поверхні планети через її середню щільність \ (\ rho \). Для цього запишемо формулу його визначення:
Масу планети знайдемо як добуток щільності на об'єм, а обсяг висловимо через радіус, оскільки планета є сферичної.
\ [M = \ rho \ cdot V = \ frac \ pi \ rho \]
Тепер висловимо доцентровийприскорення \ (a_ц \) через період обертання. Для цього запишемо формулу визначення центростремительного прискорення через кутову швидкість обертання і формулу зв'язку кутової швидкості обертання з періодом обертання планети:
Підставами вираження (3) і (4) в рівність (2):
Висловимо з отриманого рівність період \ (T \), отримаємо рішення задачі в загальному вигляді:
Відповідь: 160 хв.
Якщо Вам сподобалася завдання і її рішення, то Ви можете поділитися нею з друзями за допомогою цих кнопок.