надзвичайна арифметика
До арифметичних дій ми звикли настільки, що виконуємо їх автоматично, майже не думаючи про те, що ми робимо. Але ті ж дії зажадають від нас чималої напруги, якщо ми побажаємо застосувати їх до чисел, написаним не по десятковій системі. Спробуйте, наприклад, виконати додавання наступних двох чисел, написаних по пятеричной системі:
Складаємо за розрядами, починаючи з одиниць, тобто праворуч: 3 + 2 дорівнює 5; але ми не можемо записати 5, тому що такої цифри в пятеричной системі не існує: 5 є вже одиниця вищого розряду. Значить, в сумі зовсім немає одиниць; пишемо 0, а 5, тобто одиницю наступного розряду, утримуємо в розумі. Далі, 0 + 3 = 3, та ще одиниця, утримана в розумі, - всього 4 одиниці другого розряду. У третьому розряді отримуємо 2 + 1 = 3. У четвертому 4 + 2 дорівнює 6, тобто 5 + 1; пишемо 1, а 5, тобто одиницю вищого розряду, відносимо далі вліво.
Шукана сума = 11340.
Надаємо читачеві перевірити це складання, попередньо переводячи зображені в лапках числа в десяткову систему.
Точно так же виконуються і інші дії. Для вправи наводимо далі ряд прикладів, число яких читач, при бажань, може збільшити самостійно:
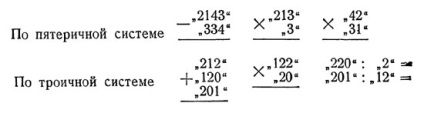
За пятеричной системі: "1304", "+1144", "2402".
При виконанні цих дій ми спочатку подумки зображуємо написані числа в звичній нам десятковій системі, а отримавши результат, знову зображуємо його в необхідній недесяткових системі. Але можна зробити і інакше: скласти "таблицю складання" і "таблицю множення" в тих же системах, в яких дано нам числа, і користуватися ними безпосередньо. Наприклад, таблиця додавання в пятеричной системі така:
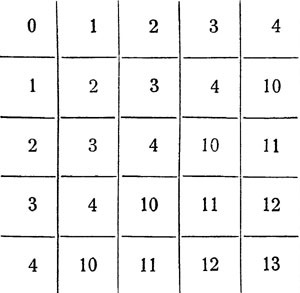
За допомогою цієї таблички ми могли б скласти числа "4203" і "2132", написані в пятеричной системі, набагато менш напружуючи увагу, ніж при способі, застосованому раніше.
Спрощується також виконання віднімання.
Складемо і таблицю множення ( "піфагорових" *) для пятеричной системи:
* (Піфагор (VI століття до нашої ери) - давньогрецький філософ; займався також математикою і теорією музики.)
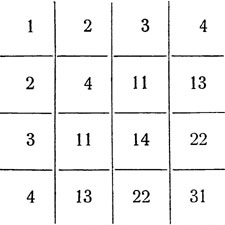
Маючи цю табличку перед очима, ви знову-таки можете полегшити собі працю множення (і ділення) чисел в пятеричной системі, як легко переконатися, застосувавши її до наведених вище прикладів. Наприклад, при множенні
розмірковуємо так: тричі три "14" (з таблиці); 4 пишемо, 1 - в розумі. 1 на 3 дає 3, та ще 1, - пишемо 4. Двічі три = "11"; 1 пишемо, 1 переносимо вліво. Отримуємо в результаті "тисячі сто сорок чотири".
Чим менше підставу системи, тим менше і відповідні таблиці додавання і множення. Наприклад, для троичной системи обидві таблиці такі:
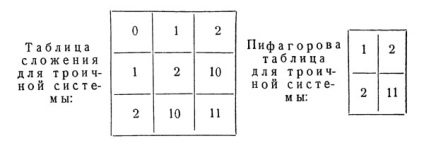
Їх можна було б відразу ж запам'ятати і користуватися ними для виконання дії. Найменші таблиці додавання і віднімання виходять для двійкової системи:
За допомогою таких-то простих "таблиць" можна виконувати в двійковій системі всі чотири дії. Множення в цій системі, по суті, як би і зовсім немає: адже помножити на одиницю - значить залишити число без зміни; множення ж на "10", "100", "1000" (тобто на 2, 4, на 8) зводиться до простого приписування справа відповідного числа нулів. Що ж стосується складання, то для виконання його потрібно пам'ятати тільки одне, що в двійковій системі 1 + 1 == 10. Чи не правда, ми з повною підставою назвали раніше двійкову систему найпростішою з усіх можливих? Довготи чисел цієї своєрідної арифметики скупається простотою виконання над ними всіх арифметичних дій. Нехай потрібно, наприклад, помножити:
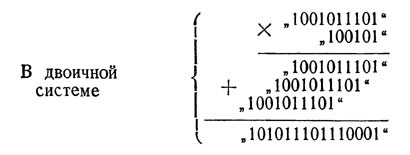
Виконання дії зводиться тільки до переписування довгих чисел в належному розташуванні: це вимагає незрівнянно менших розумових зусиль, ніж множення тих же чисел в десятковій системі (605 X Х37 = 22385).
Якби у нас була прийнята двійкова система, вивчення письмового числення вимагало б найменшого напруження думки (зате - найбільшої кількості паперу і чорнила). Однак в усному рахунку двоичная арифметика по зручності виконання дій значно поступається нашій десяткової.
Наведемо також приклад дії поділу, виконаного в двійковій системі числення:
У звичній нам десятковій системі дію це мало б такий вигляд:
Ділене, дільник, приватне і залишок в обох випадках, по суті, однакові, але проміжні викладки різні.