Будь-яке натуральне число завжди ділиться на 1 і на саме себе. Число 2 - найменше просте число. Це єдине парне просте число, інші прості числа - непарні.
Простих чисел багато, і перше серед них - число 2. Однак немає останнього простого числа.
Але багато натуральні числа діляться без остачі ще й на інші натуральні числа.
- число 12 ділиться на 1, на 2, на 3, на 4, на 6, на 12;
- число 36 ділиться на 1, на 2, на 3, на 4, на 6, на 12, на 18, на 36.
Числа, на які число ділиться без остачі (для 12 це 1, 2, 3, 4, 6 і 12) називаються дільниками числа. Дільник натурального числа a - це таке натуральне число, яке ділить дане число a без залишку. Натуральне число, яке має більше двох дільників, називається складовим. Зверніть увагу, що числа 12 і 36 мають спільні дільники. Це числа: 1, 2, 3, 4, 6, 12. Найбільший з подільників цих чисел - 12.
Загальний дільник двох даних чисел a і b - це число, на яке діляться без залишку обидва даних числа a і b. Загальний дільник кількох чисел (НСД) - це число, що служить дільником для кожного з них.
Коротко найбільший спільний дільник чисел a і b записують так:
Приклад. НСД (12; 36) = 12.
Подільники чисел в запису рішення позначають великою літерою «Д».
Числа 7 і 9 мають тільки один спільний дільник - число 1. Такі числа називають взаємно простимічі Слами.
Взаємно прості числа - це натуральні числа, які мають тільки один спільний дільник - число 1. Їх НОД дорівнює 1.
Найбільший спільний дільник (НСД), властивості.
- Основна властивість: найбільший спільний дільник m та n ділиться на будь-який спільний дільник цих чисел. Приклад. для чисел 12 і 18 найбільший спільний дільник дорівнює 6; він ділиться на всі загальні дільники цих чисел: 1, 2, 3, 6.
- Слідство 1: безліч спільних дільників m і n збігається з безліччю подільників НСД (m. N).
- Слідство 2: безліч загальних кратних m і n збігається з безліччю кратних НОК (m. N).
- Якщо m ділиться на n. то НСД (m. n) = n. Зокрема, НОД (n. N) = n.
- - загальний множник можна виносити за знак НСД.
- Якщо, то після ділення на числа стають взаємно простими, тобто,.
Це означає, зокрема, що для приведення дробу до нескоротних увазі треба розділити її чисельник і знаменник на їх НСД.
- Мультипликативность: якщо взаємно прості, то:
- Найбільший спільний дільник чисел m і n може бути визначений як найменший позитивний елемент безлічі всіх їх лінійних комбінацій:
і тому представимо у вигляді лінійної комбінації чисел m і n:
.
Це співвідношення називається співвідношенням Безу. а коефіцієнти u і v - коефіцієнтами Безу. Коефіцієнти Безу ефективно обчислюються розширеним алгоритмом Евкліда. Це твердження узагальнюється на набори натуральних чисел - його сенс в тому, що підгрупа групи, породжена набором, - циклічна і породжується одним елементом: НОД (a1. A2. .... An).
Обчислення найбільшого загального дільника (НСД).
Ефективними способами обчислення НСД двох чисел є алгоритм Евкліда і бінарнийалгорітм. Крім того, значення НСД (m, n) можна легко обчислити, якщо відомо канонічне розкладання чисел m і n на прості множники:
де - різні прості числа, а й - невід'ємні цілі числа (вони можуть бути нулями, якщо відповідне просте відсутній в розкладанні). Тоді НОД (m, n) і НОК (m, n) виражаються формулами:
Якщо чисел більше двох:, їх НОД знаходиться за наступним алгоритмом:
- це і є шуканий НСД.
Також, для того, щоб знайти найбільший спільний дільник. можна розкласти кожне із заданих чисел на прості множники. Потім виписати окремо тільки ті множники, які входять в усі задані числа. Потім перемножуємо між собою виписані числа - результат перемноження і є найбільший спільний дільник.
Розберемо покроково обчислення найбільшого загального дільника:
1. Розкласти подільники чисел на прості множники:
Обчислення зручно записувати за допомогою вертикальної риси. Зліва від межі спочатку записуємо ділене, праворуч - дільник. Далі в лівому стовпчику записуємо значення приватних. Пояснимо відразу на прикладі. Розкладемо на прості множники числа 28 і 64.
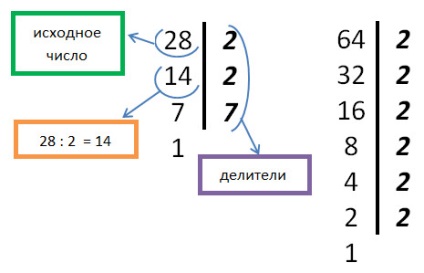
2. Підкреслюємо однакові прості множники в обох числах:
28 = 2 • 2 • 7
64 = 2 • 2 • 2 • 2 • 2 • 2
3. Знаходимо твір однакових простих множників і записуємо відповідь:
НСД (28; 64) = 2 • 2 = 4
Відповідь: НСД (28; 64) = 4
Оформити знаходження НСД можна двома способами: в стовпчик (як робили вище) або «в рядок».
Перший спосіб запису НСД:
Знайти НСД 48 і 36.
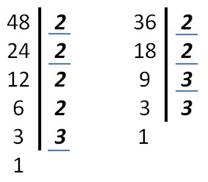
НСД (48; 36) = 2 • 2 • 3 = 12
Другий спосіб запису НСД:
Тепер запишемо рішення пошуку НСД в рядок. Знайти НСД 10 і 15.