Під впливом зовнішніх сил тіло змінює форму і об'єм, в результаті цього в ньому виникають внутрішні сили, які прагнуть до відновлення колишньої форми. Поверхнева щільність сили, що виникає в кожному елементі тіла, називається напругою.
напруга # 963; - величина векторна. Вона залежить від внутрішніх властивостей породи (сил і характеру зв'язків між частинками), форми зразка і від дії зовнішніх сил. Сили, що діють в одному напрямку, викликають в зразку лінійне напружений стан, діючі в двох напрямках, але в одній площині - плоский напружений стан, а в інших випадках - об'ємний напружений стан.
В абсолютно щільною породі напруги розраховуються за формулою:
де S - площа, на яку впливає сила.
У пористих породах
де S0 - площа контакту мінеральних зерен; Sп - площа, зайнята порами.
Напруги концентруються тільки в області контакту мінеральних зерен
Тому зі збільшенням пористості, тріщинуватості і виветрелості, при інших рівних умовах, напруги в породі зростають. Ступінь зростання справжніх напруг в пористої породі виявляється ще більше через місцеву концентрації напружень, що виникає в кутах тріщин і пор.
Розглянемо тіло довільної форми, що знаходиться в рівновазі під дією прикладених до нього зовнішніх сил. Розсічений подумки розглянуте тіло будь-якої поверхнею на дві частини. Замінимо дію однієї частини доданої до перетину внутрішніми силами, так щоб решта перебувала в рівновазі. Взагалі кажучи, внутрішні сили нерівномірно розподілені по площі перетину. Виділимо на перетині елементарну площадку на яку діє сила.
У цьому випадку відношення
називається вектором напруги на майданчику.
Розсікаючи розглянуте тіло площинами паралельними прямоуголний системі координат, можна прийти до елементарного кубику на кожну зовнішню грань якого діють свій вектор напружень. Проекції цих векторів на осі координат представляють дев'ять компонентів напружень - два дотичних і одне нормальне на кожній грані кубика (рис. 10). Всі вони представляють одну фізичну величину, яка називається тензором напружень.
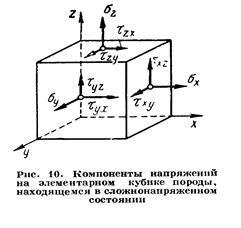
Запис тензора напружень має такий вигляд
Сума моментів щодо будь-якого ребра розглянутого елементарного кубика повинна бути дорівнює нулю. Звідси випливає закон парності дотичних напружень:
Таким чином, напружений стан твердого тіла в будь-якій площині можна охарактеризувати діючими в ньому нормальними і дотичними напруженнями. Вони взаємопов'язані і можуть бути розраховані шляхом складання векторів. На рис.11 наведено приклад навантаження зразка осьовим () і бічним () зусиллями (). Для відшукання нормального () і дотичного () напруги, що діє на похилій площадці, розташованої під кутом. можна скористатися графічним методом за допомогою кіл напруг Мора, які будуються в такий спосіб (рис. 11): на осі абсцис відкладають максимальне і мінімальне значення нормальних напружень, що діють на зразок; на різниці відрізків, як на діаметрі, будується півколо.
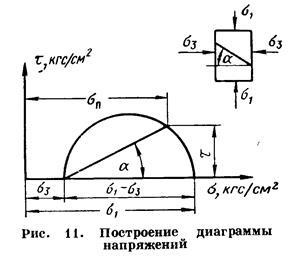
Значення дотичного і нормального напруг в будь-якій точці зразка можуть бути визначені, якщо заданий кут нахилу площини, в якій визначаються напруги. Під цим кутом з точки перетину кола з абсцисою проводять пряму до перетину з півколом. Координати точки перетину півкола з прямою чисельно дорівнюють значенням певних напружень. Кожному приватному значенням напруженого стану відповідає своє коло напружень.
Напруження в породах можуть виникати під впливом не тільки зовнішніх сил, але і різних фізичних полів. Напруги бувають термічні, усадочні, обумовлені нерівномірним охолодженням обсягу, залишкові, що виникають в результаті нерівномірного розподілу напружень через місцеву плинності матеріалу, та ін. На ці напруги накладаються напруги від зовнішнього впливу, які можуть або збільшувати, або зменшувати їх.
Під впливом зовнішніх сил гірська порода зазнає змін лінійних розмірів, обсягу або форми, які називаються деформаціями.
Деформації, відповідні нормальним напруженням, виражаються через відносну зміну і лінійних розмірів зразка
Де l 'і l - довжина зразка відповідно в деформованому і недеформованому стані.
Відносні деформації, відповідні дотичним напруженням, виражаються через тангенс кут зсуву граней елементарного обсягу зразка. Зважаючи на малість кута справедливо співвідношення.
Деформації подовження і зсуву можна розкласти на складові по осях координат. В теорії пружності, (розділ теорія деформацій) дається висновок тензора деформацій. визначає стан деформації в будь-якій точці тіла: