За рахунок різниці в потоках тепла в глиб тіла і на поверхню температура останньої безперервно зростає. Одночасно, звичайно, зростає потік і всередину тіла, збільшується температура і внутрішніх ділянок, але кілька відстаючими темпами. При нескінченному часу температури печі, поверхні тіла і його центру, природно, порівнюються.
На практиці за багато десятиліть склалися певні прийоми рахунку без обчислювальної техніки. Для цього використовують метод безрозмірних змінних і попередньо розраховані номограми. Сенс безрозмірних змінних в тому, що для абсолютно різних тіл і процесів, якщо вони будуть описуватися одними і тими ж значеннями безрозмірних змінних, досліджувані явища будуть подібними.
Вуравненіі (5.3.1) всевелічіниімеютразмерность. Однакоодну безрозмірну величину, в яку входять коефіцієнти тепловіддачі і теплопровідності, і яку можна використовувати для розрахунку, ми вже отримали - це критерій Біо Bi. Другу безрозмірну ха-
характеристику - безрозмірний час. або критерій Фур'є Fo, отримаємо з самого диференціального рівняння нестаціонарної дифузії.
Сенс процесу отримання критерію Bi зводиться до заміни диференціалів в рівнянні на самі змінні. Формально це виглядає як просте викреслювання знаків диференціалів. Такий прийом носить назву методу Гухман. Таким чином, прибираючи знаки диференціала з рівняння (5.1.10), отримуємо співвідношення:
T / τ = a · T / L 2,
в якому через Т ∞ позначена температура навколишнього тіло середовища (стінок печі), а Т о є початкова температура тел.
Для практичних розрахунків без засобів обчислювальної техніки використовують номограми, в яких графічно відображена функціональна залежність безрозмірної температури θ від безрозмірного часу Fo для різних значень критеріїв Біо. Обговорювані функції різні для центру і поверхні тіла. Відрізняються вони і для різних форм тіла, наприклад плоского і циліндричного. Як характерний розміру для плоских тіл беруть зазвичай половину його товщини (зазвичай нагрів буває двостороннім). Для циліндричних тіл за характерний розмір завжди вибирають його радіус. Тобто маємо Bi = α R / λ. Номограми для поверхні і центру циліндричних тіл, як приклади, наведені на рис. 5.3.1 і 5.3.2. Як бачимо, вони мають істотними відмінностями в численних значеннях.
На практиці зазвичай зустрічаються два типи завдань.
У першому з них потрібно визначити час нагрівання тіла до заданої температури Т кін; зазвичай за такий час вибирається час нагрівання центру тіла. Алгоритм розрахунку наступний.
♦ Розраховуємо критерій Біо для тіла: Bi = α · L / λ і визначаємо відповідну пряму на номограмі для центру тіла.
♦ З Т кін розраховуємо необхідну безрозмірну температуру:
θ = (T ∞ - T кін) / (T ∞ - T o)
♦ Відкладаючи ординату θ на номограмі і проводячи пряму до перетину з лінією номограми для даного значення критерію Біо, отримуємо абсциссу - значення безрозмірного часу Fo.
♦ За формулою τ = Fo · L 2 / a розраховуємо звичайне времявсекундах.

Мал. 5.3.1. Номограма співвідношень безрозмірних величин для поверхні циліндра
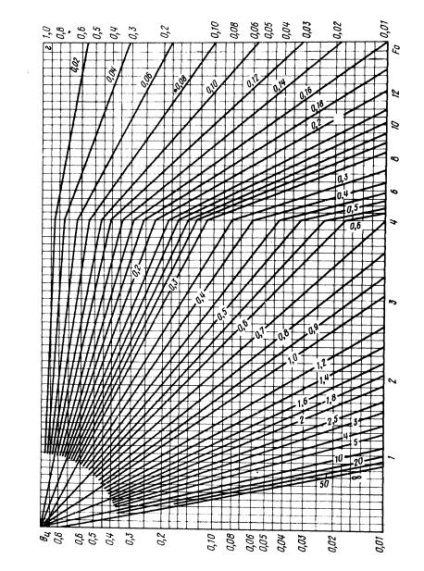
Мал. 5.3.2. Номограма співвідношень безрозмірних величин для центру циліндра
Другий часто зустрічається завданням є визначення тимчасових кількісних залежностей нагріву тіла на поверхні і в його середині. Тут алгоритм розрахунку такої.
♦ Розраховуємо критерій Біо для тіла: Bi = α. L / λ і визначаємо відповідні прямі на номограмах для поверхні і центру тіла.
♦ Задаємо набір значень природного часу процесу τ. сек.
♦ Обчислюємо відповідний набір безрозмірних часів для поверхні і центру тіла: Fo = τ. a / x 2. які задають абсциси на номограмі.
♦ По перетину перпендикуляра до осі абсцис з прямою, що відповідає значенню критерію Біо, знаходимо ординати - значення безрозмірних температур θ для поверхні і центру тіла.
♦ Обчислюємо середні температури за формулою: Т = T ∞ - θ. (T ∞ - T о) для поверхні Т пов і центру тіла Т ц.
♦ Будуємо графіки часової залежності температур для поверхні Т пов і центру тіла Т ц.
Приклад. Злитки міді і нікелю товщиною 300 мм нагріваються від початкової температури 20 до 500 ° С. Температура в печі 550 ° С. Нагрівання проводиться з одного боку. Коефіцієнт тепловіддачі в печі 100 [Вт / (м 2 К)]. Визначити час нагрівання мідного і нікелевого злитків до заданої температури і перепад температури по товщині злитка.
0. Проведемо основні визначення необхідних констант.
За довідником фізико-хімічних величин знаходимо щільність міді, рівну 8,92. 10 3 [кг / м 3], нікелю 8,63. 10 3 [кг / м 3]. Теплоємність міді при середній температурі металу 260 ° С дорівнює 407 [Дж / (кг. К)], нікелю - 472 [Дж / (кг · К)]. Теплопровідність міді при середній температурe дорівнює 376 [Вт / (м · К)], нікелю - 57 [Вт / (м · К)]. При односторонньому нагріванні за характерний розмір приймаємо
повну товщину злитка.
1. Обчислюємо значення критеріїв Біо.
a. Для міді маємо: Вi = (100 · 0,3) / 376 = 0,08 <<0,25. б. Для никеля Вi = (100·0,3)/57 = 0,53> 0,50.
2. Оскільки для нашого злитка міді Вi <0,25, время нагрева рассчитываем по уравнению для тонкого тела. Принимая для простоты поверхность нагрева равной 1 м 2 :
Нагрівання нікелю буде протікати повільніше міді.
Знайдемо температуру, яку буде мати верхня поверхня злитка Ni в кінці процесу нагріву. Для цього з номограми за значеннями Вi і Fо знаходимо θ пов = 0,083. Температура верхньої по-
поверхні буде: Т пов = 550 - 0,083. (550 - 20) = 506 ° С. Таким обра-
зом, температура верхній поверхні злитка буде всього на 6 ° С вище температури нижньої поверхні, що пов'язано з усе-таки не дуже великим значенням критерію Біо (0,53).
1. Виведіть рівняння нестаціонарної теплопровідності, ґрунтуючись на законі Фур'є.
2. У чому сенс коефіцієнта температуропровідності?
3. Який фізичний зміст рішення рівняння нестаціонарної теплопровідності (дифузії)?
4. Які Ви знаєте типи крайових умов? Там, де це початкова умова?
5. Напишіть гранична умова тепловіддачі (массоотдачи) по Ньютону. У чому його недолік?
6. Проілюструйте використання методу Гухман на прикладі введення безрозмірного часу.
7. Як вводяться безрозмірні час і температура?
8. Що характеризує критерій Фур'є?
6. Е лементи ГІДРОДИНАМІКИ
Режими течії рідин і газів. Прикордонні шари. Наближення Ленгмюра. Фізичний сенс шарів. Зовнішня і внутрішня завдання. Обертовий диск.
При перебігу середовища вздовж нерухомої поверхні її швидкість u (x, у) по перетину потоку не залишається постійною. Розглянемо двомірну задачу і направимо вісь X уздовж поверхні, а вісь Y - перпендикулярно до неї. Шар середовища, що прилягає до поверхні пластини (y = 0), нерухомий: u (x, 0) = 0. Його товщина залежить від відстані, пройденого середовищем від передньої кромки пластини. Ця умова є граничною умовою, що використовуються для вирішення диференціального рівняння руху середовища. При збільшенні y швидкість зростає від нуля до деякого постійного значення, рівного швидкості середовища в ядрі потоку u. За товщину динамічного прикордонного шару приймають відстань y = δ о. на якому досягається значення швидкості, що дорівнює 0.99 від швидкості в ядрі потоку.
Зростання швидкості в прикордонному шарі говорить про переважне вплив в цьому шарі сил внутрішнього тертя (в'язкості). За межами прикордонного шару дію цих сил не роблять істотного впливу, і інерційні сили переважають над силами в'язкості. Згідно допущенню Ленгмюра, швидкість в прикордонному шарі зростає лінійно з віддаленням від поверхні пластини або іншого обтічного тіла. Це, взагалі кажучи, справедливо тільки для малої товщини шарів; реальний розподіл швидкості - параболічне, але зазвичай цим нехтують, за винятком встановленого (стабілізованого) течії середовища, коли вже не можна говорити про наближення прикордонного шару.
Використовуючи поняття товщини динамічного прикордонного шару, можна визначити поняття зовнішньої завдання. в умовах зовнішньої завдання товщина прикордонного шару значно менше відстані до будь-якої іншої поверхні.
У внутрішній задачі при сталому перебігу середовища дію сил в'язкості проявляється у всьому потоці між ограничи-
вающими стінками. У цьому випадку на деякій довжині l гідроді-
наміческіх початкового ділянки прикордонні шари змикаються (рис. 6.1.1) і встановлюється стабілізований режим розподілу швидкості.
Мал. 6.1.1. Профіль швидкостей в сталому режимі течії рідини:
а - ламінарний потік; б - турбулентний
Рівняння прикордонного шару можна отримати з рівняння руху середовища і рівняння суцільності при допущенні малої товщини прикордонного шару в порівнянні із значенням координати x вздовж нерухомої поверхні, коли можна опустити члени д 2 u / дx 2. але слід залишити члени д 2 u / дy 2. В іншому випадку поняття прикордонного шару втрачає сенс і для визначення поля швидкостей необхідно вирішувати суворі диференціальні рівняння з відповідними умовами однозначності, тобто граничними і початковими умовами. Загальним для всіх випадків обтікання нерухомою поверхні буде умова прилипання. тобто нерухомості середовища у поверхні: u (0) = 0.
Вирішивши відповідне рівняння, для визначення товщини прикордонного шару в залежності від відстані x від передньої кромки нерухомою поверхні до поточної точки отримаємо вираз:
δ про (х) = A · (х ν / u) 0.5.
Експериментально певний коефіцієнт пропорційності А для ламінарного поздовжнього обтікання плоскої пластини дорівнює 5,6; для труби А одно 2,44.
Звідси можна легко отримати формулу для розрахунку довжини, на якій стабілізується потік, тобто довжину l о. на якій має
сенс говорити про прикордонному шарі:
Тобто для нього товщина прикордонного шару не залежить від відстані від осі обертання. Обертові диски дуже ефективно використовують для дослідження кінетики гетерогенних процесів під на-
званням метод однаково доступний поверхні. Коефіцієнт А тут дорівнює 3,6.
Для методу Чохральського, де монокристали вирощуються з розплаву з обертанням не тільки кристала, нижня поверхня якого і є обертовим диском, але і зустрічним обертанням середовища (тигля), коефіцієнт А дорівнює 5,0; за швидкість обертання беруть кутову швидкість обертання кристала.
6.2. Діффузіоннийітепловой погранічниеслоі
Робочі формули в теорії подібності. Співвідношення товщини прикордонних шарів для газів і рідин.
Якщо на твердій поверхні (вісь Х), уздовж якої рухається хімічно активне середовище, протікає гетерогенна реакція, то концентрація реагентів у поверхні C | y = о = С пов може значно відрізнятися від їх концентрацій в ядрі потоку - основному обсязі середовища. Ці концентрації в ядрі потоку відразу після зовнішнього кордону гідродинамічного прикордонного шару при великих значеннях критерію Пеклі і великих швидкостях руху середовища залишаються постійними. У той же час усередині прикордонного гідродинамічного шару концентрація змінюється, в зв'язку з чим можна говорити про диффузионном прикордонному шарі. Якщо поверхню і оточуюча середовища мають різні температури, то можна говорити і про тепловому прикордонному шарі - природно, коли він лежить всередині гідродинамічного, і, звичайно, тільки для зовнішньої задачі, коли взагалі має сенс говорити про прикордонні шарах.
Можна вважати, що в межах дифузійного (теплового) прикордонного шару массообмен (теплопередача) йде тільки молекулярними механізмами згідно із законом Фіка (Фур'є), а поза ним - конвекцією. Тобто зовнішні кордони дифузійного або теплового погра-
кових шарів лежать всередині або в крайньому випадку на зовнішньому кордоні гідродинамічного шару - там, де швидкість руху середовища вже має помітну величину і повністю визначає кількісну міру перенесення речовини або теплової енергії. Природно, що товщини дифузійного і теплового шарів пов'язані з товщиною гідродинамічного шару. Функціонально цей зв'язок виражається рівнянням для дифузійного шару:
δ j (х) = A · δ про (х) · (D j / ν) -0.33.
а для теплового:
δ т (х) = A · δ про (х) · (а / V) -0.33.
де величина А залежить від виду і характеру завдання. Для поздовжнього обтікання пластини А дорівнює 3; для диска, що обертається воно дорівнює 1,6; для методу Чохральського А = 2,2.
Для газів значення товщини гідродинамічного, теплового і дифузійного шарів близькі по порядку величин, і найчастіше товщина гідродинамічного шару в 2-4 рази більше, ніж товщина теплового або дифузійних шарів. Для рідин ця величина складає зазвичай 5-10 разів по відношенню до диффузионному шару. Але для теплового шару в розплавах напівпровідників картина зворотна - теплової прикордонний шар значно більше гідродинамічного. Причина явища - дуже велика теплопровідність розплавів напівпровідників (і рідких металів) за рахунок електронної складової.
Оскільки дифузний і теплової шари по своєму фізичному сенсу лежать всередині гідродинамічного, то вони можуть існувати для внутрішньої задачі і на кілька великих відстанях уздовж обтічного об'єкту, ніж початковий гідродинамічний ділянку, перебуваючи всередині вже стабілізованого потоку.
При стабілізованому параболическом профілі швидкості товщина дифузійного шару розраховується за рівнянням:
δ j (х) = 0.94 · (Vhx / U) -0.33 · (D j / v) -0.33. (6.2.1)
де h - відстань від пластини до найближчої нерухомої стінки по нормалі; величина U дорівнює середній швидкості руху середовища в реакторі. Для теплового шару в (6.2.1) D j потрібно просто замінити на коефіцієнт температуропровідності а.
З (6.2.1) легко визначити максимальну довжину пробігу газової суміші вздовж реактора, на якій ще можна говорити про існування теплового або дифузійного прикордонного шару. тобто,