Визначення. Функція називається нескінченно-малої в точці. якщо.
Функція називається нескінченно-великий в точці. якщо.
Це поняття можна застосувати до функції «взагалі», без вказівки точки. Не буває просто «нескінченно-малої функції», буває тільки «нескінченно-мала функція в точці». Це властивість поведінки функції в конкретній точці. Так, є нескінченно-малої прі.
Очевидно, що якщо беск-мала в точці, то є нескінченно-великий в тій же точці.
Приклад. Фкнкція є нескінченно малою в точках і 1 і нескінченно великою в точці 2.
Нескінченно малі називаються порівнянними. якщо існує хоча б один з меж або.
Якщо. причому і. то дві функції називаються нескінченно-малими ОДНОГО ПОРЯДКУ малості. До речі, тоді. тобто обидва межі рівні кінцевим числах, а не. Якщо було б то другий межа була б.
Якщо при цьому. тобто . то дві нескінченно малі називаються ЕКВІВАЛЕНТНИМІЕто окремий випадок тієї ситуації, коли вони одного порядку.
Якщо то називається нескінченно-малої вищого порядку, ніж.
Приклад. . Функції і одного порядку в точці 0.
Приклад. . а також ,
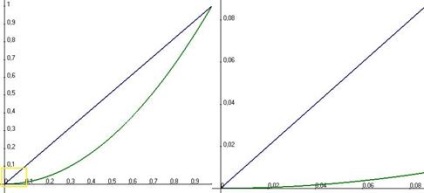
тобто більш високого порядку, ніж. І хоча вони обидві прагнуть до 0, але швидкість цього процесу кардинально відрізняється. Якщо розглянути їх графіки при великому збільшенні близько початку координат, то парабола майже не відрізняється від осі 0х.
Третя ступінь - ще більш високого порядку, вона буде проходити нижче, ніж парабола. Як ми бачимо, хоч і всі вони прагнуть до 0, але ці нулі як би зовсім різної сили.