Нормальне рівняння прямої на площині

Головна | Про нас | Зворотній зв'язок

Розглянемо довільну пряму. Відновимо з початку координат вектор нормалі до даної прямої і одиничний вектор. напрямок якого збігається з напрямком вектора. Нехай (якщо пряма проходить через початок координат, то). Нехай - кут між вектором і віссю абсцис (в разі, коли в якості можна взяти будь-яке значення). Так як - одиничний вектор, то його координати, рівні його проекція на координатні осі, мають вигляд:

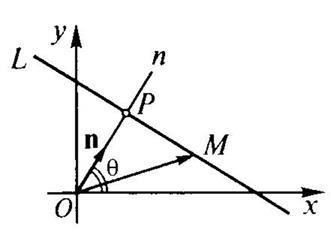
Очевидно, що точка лежить на даній прямій тоді і тільки тоді, коли проекція вектора на вісь, яка визначається вектором. дорівнює. Так як . то отримуємо

Отже, рівняння прямої може бути записано у вигляді:

Таке рівняння називається нормальним рівнянням прямої.

Розглянемо довільну точку. Нехай - відстань від цієї точки до прямої. Відхиленням точки від цієї прямої називається відстань. взяте зі знаком плюс, якщо ця точка і початок координат лежать по різні боки від даної прямої, і взяте зі знаком мінус, якщо ця точка і початок координат лежать по одну сторону від прямої.

З'ясуємо геометричний зміст лівої частини нормального рівняння. Спроектуємо довільну точку на вісь, яка визначається вектором. Нехай - отримана проекція, а - точка перетину прямої з даної прямої. Очевидно, що відхилення точки від даної прямої дорівнює величині вектора. Відповідно отримуємо:

Таким чином, отримуємо правило: для знаходження відхилення точки від даної прямої слід в ліву частину нормального рівняння цієї прямої підставити координати цієї точки.

З'ясуємо, як із загального рівняння отримати нормальне рівняння. Нехай дано рівняння

Знайдемо множник. при множенні на який загальне рівняння перетвориться в нормальне. При цьому повинно виконуватися:

Зводячи в квадрат перші два рівності і потім, складаючи їх, отримаємо

Так як відстань завжди неотрицательно, то з третього рівності системи робимо висновок, що знак повинен бути протилежний знаку. Отже, для приведення загального рівняння до нормального вигляду слід помножити його на нормуючий множник, який визначається рівністю. при цьому знак в останній формулі вибирається протилежним знаку коефіцієнта. Відповідно до цього отримуємо формулу для знаходження відстані від точки до прямої:

Приклад. Написати рівняння прямої, що проходить через точки і. Привести це рівняння до нормального вигляду і з'ясувати перетинає ця пряма відрізок, що з'єднує точки і.

# 8710; Скористаємося канонічним рівнянням прямої, що проходить через задані дві точки:

Помноживши на число 12 обидві частини отриманого рівняння, отримаємо загальне рівняння:

Для приведення його до нормального вигляду знайдемо нормирующий множник, вибравши його знак, протилежний знаку коефіцієнта:

Помноживши на цей множник, будемо мати нормальну рівняння розглянутої прямий:

Щоб з'ясувати, перетинає ця пряма відрізок, що з'єднує точки і. знайдемо відхилення цих точок щодо цієї прямої, підставивши їх координати в ліву частину нормального рівняння:

Так як відхилення точок і мають протилежні знаки, то вони лежать по різні боки щодо даної прямої. Таким чином, ця пряма перетинає відрізок, що з'єднує зазначені точки. ▲