Андрій Чернов. Нотатки про вічне
Пентаграма ПО Менделєєва
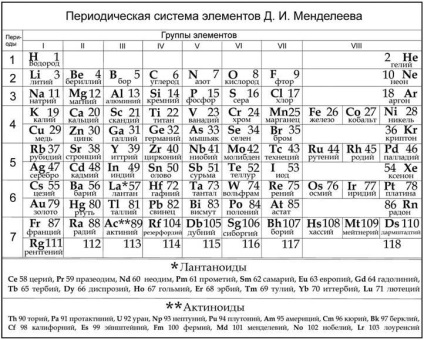
Н аходка С. А. Родіонової (див. Замітку «Базова модель тРНК) вимагає перевірки на якомусь іншому (але настільки ж фундаментальному) матеріалі. Згадаймо основи шкільної хімії і представимо у вигляді графічної моделі Періодичну таблицю Д. І. Менделєєва. Сьогодні вже відкриті 112, 114, 116 і 118-й елементи, а тому будемо виходити з того, що в VII періоді 32 елемента (як і в попередньому).
Якщо модель тРНК - хрест (у біологів прийнято політкоректно називати його «листом конюшини»), то двовимірна модель Періодичного закону - обтяжена двома протуберанцями пентаграма [1]. У структурі таблиці Менделєєва дві яскраво виражених точки перегину (57 лантан і 89 актиній), з них і починаються протуберанці - лантаноїди і актиноїди. Формально їм немає місця в таблиці. Ці два окремих сімейства записуються, як правило, під таблицею.
Згадаймо, що золотий перетин базової тРНК припадає на 47 нуклеотид і після нього можливий протуберанець - ланцюжок додаткових елементів. Але і золотий перетин від числа базових елементів семи періодів таблиці Менделєєва (без протуберанців) - точка, що передує першому протуберанці:
Назвемо це першим збігом. Воно говорить про те, що довжина таблиці Менделєєва має бути обмежена 118 елементами.
Визначимо точку золотого перетину для VII повних періодів таблиці:
Це тантал, хімічно і корозійно стійкий, а ще й жаростійкий елемент таблиці. На перший погляд може здатися, що він не перебуває в структурній точці і для нашого сюжету абсолютно даремний. Однак це не так, адже в тРНК один розвинений протуберанець, а в таблиці Менделєєва два. Там золото припадає на вихідний елемент протуберанця, тут же № 73 лежить між вихідними і якраз точно посередині. Ось і середньоарифметичне між двома точками початку протуберанців вказує на тантал:
Значить можна говорити про другий збігу.
Оскільки номер елемента безпосередньо пов'язаний з його атомним вагою, фізичний зміст № 73 той же, що у шнурка, за який антична Феміда тримає свої ваги: це точка рівноваги.
Тантал - гарне ім'я для точки золотий пропорції і рівноваги, якщо згадати, що цей міфологічний герой був приречений грецькими богами на вічні муки - стояв по підборіддя у воді і не міг напитися, а обтяжені плодами гілки злітали вгору, коли він простягав до них руки. За √2 тантал пов'язаний зі 104 елементом, першим після другого протуберанця. (Третє збіг.) В каламбурного танталові інтригу втягнуто і число π. оскільки 73. π / 2 = 46,5 → 47 (знову структурна точка - початок другого рядка VI періоду; ім'я елемента - срібло). У природі тантал зустрічається спільно з ніобієм (41), який названий по Ниобе, дочки міфологічного Тантала. Властивості ніобію і танталу дуже схожі. Але середньоарифметичне танталу і ніобію - перша точка перегину моделі, вихідний для першого протуберанця лантан (57). При цьому і 57. √2 = 40,3 → 41. А по √5 ніобій пов'язаний з числом базових елементів, адже 90. √5 = 40,2 → 41, тобто структурно ніобій відповідає початку антикодону в тРНК і ділить число базових елементів в пропорції (√5 -1) до 1.
З Олот пропорція по визначенню - точка геометричного рівноваги щодо і цілого з його частинами, і самих частин. Але в Періодичний закон це точка і геометричного, і фізичного рівноваги між вихідними для протуберанців лантаном і актинієм.
• Графічна модель Періодичної системи Менделєєва.
В хімічній літературі ніобій і тантал зазвичай і розглядають як певну нерозлучну пару (див. «Ниобий» по Вікіпедія).
Але якщо взяти 90 базових елементів таблиці, то ніобій, це 90 / √5.
Отже, по пропорції √5 від числа базових елементів отримуємо ніобій, а по золотому перетину від 118 елементів - парний до ніобію тантал. Але оскільки √5 є базове число золотого перетину, це «збіг» ще раз свідчить на користь того, що таблиці Менделєєва обмежена 118-ю елементами.
НОТАТКИ НА ПОЛЯХ
Про тношеніе суми основних елементів семи періодів (без двох протуберанців) до тієї ж точки № 73 - відмінне наближення до подвійного мінорному золоту (збіг № 4):
90. 73 = 1,233 → (√5 - 1)
При 118 елементах відношення основних до суми довжин протуберанців визначено подвійним мажорних золотом:
90. (√5 + 1) = 27,8 → 28
Однак збігом це назвати не можна, тому що в тРНК дана пропорція потрапляє на неструктурної точку 28.
У базовій тРНК по √2 отмерена сума неконсервативних елементів. Число базових елементів таблиці Менделєєва (без протуберанців) також пов'язано з √2 (збіг № 5):
90. √2 - 28 = 35,6 → 36 (точка перегину, конецIVперіода)
І саме при 118 елементах √2 вказує на одне з найбільш фундаментальних властивостей таблиці Менделєєва:
118. √2 = 83,4 → 84
Це перший елемент з радіоактивного хвоста таблиці - важкий і нестійкий полоній. Останній стійкий елемент в таблиці - вісмут (83). Але ставлення 118/83 ближче до √2, ніж 118/84. Отже, √2 вказує на суму стійких елементів Періодичного закону (Збіг № 6).
Перейдемо до срібного перетину.
У базовій тРНК срібне перетин доводиться на структурні точки (№ 25 - діаметр і № 52 - ціле мінус діаметр). І ще в двох випадках пари структурних точок знаходяться один від одного на відстані, рівному діаметру молекули.
При 118 елементів таблиці Менделєєва її діаметр буде дорівнює 38. Але таке відстань від 19 (початок IV періоду) до 57 елемента. (Збіг № 7.)
Обчислимо діаметр від суми базових елементів таблиці:
90: π = 28,6 → 29 (точка перегину, перший елемент другого рядка IV періоду)
Якраз 29 позицій (збіг № 8) від 57 до 86 елемента (кінець VI періоду). Але перший протуберанець і виходить з точки довжини окружності з діаметром в довжину променя пентаграми:
При цьому природа вміє пожартувати. Діаметр базового мінімуму (90 основних елементів), взятий від довжини семи повних періодів, вказує на початок другого протуберанця (збіг № 9):
Якщо таблиця завершена, то це і є точка її срібного перетину.
При цьому дві початкових точки обох протуберанців пов'язані делителем π / 2.
І так, якщо вірити пропорційної логіці гармонійних констант, Періодична таблиця повинна завершитися VII періодом. У нас просто не залишилося невмотивованих гармонійними константами структурних точок. А ті, які є, дев'ятиразовий вказують на межу з 90 + 28 елементів. І раз так, то мрії фізиків-ядерників про нову галузі ядерної стабільності надважких елементів, яка ось-ось має відкритися при переході до елементів VIII періоду, мабуть, мріями і залишаться. Надто вже закінчена картина, принципово неотличимая від тієї, що реалізована в базовій тРНК. (Про що свідчить ряд нетривіальних відповідностей), виникає при 118 елементах в таблиці.
Однак академік Ю. Ц. Оганесян пише: «Гіпотетично можливі елементи з атомними номерами до 160, можливо, до 170. Однак межа їх існування намічається значно раніше. Причина - нестабільність самого ядра »[2].
Припустимо, що існує і VIII період, і в ньому також 32 елемента (при 150 в таблиці). Тоді 121-й буде вихідним для третього протуберанця. Середньоарифметичне від 57 + 89 + 121 дасть 89 (що не дивно, оскільки тривіально), а пропорція 121. Ф 2 вкаже на початок другого рядка V періоду. Але інших зближень ми не виявимо: все гармонійні точки ляжуть «в молоко».
Але при 50 елементах в VIII періоді (18 + 18 + 14) і, відповідно, при 168 елементах таблиці виявляється:
168. √2 = 118,8 → 119
А це як раз початок VIII періоду.
Так, може бути, він і справді існує?
НОТАТКИ НА ПОЛЯХ
Але на цьому гармонійний сюжет Періодичної таблиці не закінчується.
Довжина кожного з протуберанців пов'язана з √5 - 1 з довжиною стандартного розвиненого періоду (взятого без урахування довжини протуберанця):
14 (√5 - 1) = 17,3 → 18
В тРНК множник подвійного мінорного золота визначає структурні точки II. III і IV гілок. У періодичної системи перший протуберанець завершується елементом № 71. Перший елемент після другого протуберанця - № 72. Довжина цього відрізка з точністю до четвертого знака по коми задана тим же множником подвійного мінорного золота:
89. 72 = 1,23611. → 1,23607 = √5 - 1
Цей же коефіцієнт з'єднує вихідну точку другого протуберанця (89) і перший елемент другого рядка VII періоду (111), початок і кінець першого рядка V періоду (37 і 46), він же визначає початок і кінець першого протуберанця (57 і 71), довжину другого рядка IV періоду (29 і 36), відношення початку першого протуберанця до першого елементу другого рядка VI періоду.
Придивимося до точкам, лежачим на краях променів нашої пентаграми. Елементи 111 і 79 співвідносяться з √2, а симетричні 47/29; 29/18; 18/11 по числу Ф.
Звернемо увагу на з'єднані числом Ф точки 29 і 18. Друга з них - завершення III періоду (і першого променя пентаграми). Таке і число елементів в IV - V періодах, а також, якщо знехтувати протуберанцями, в VI і VII періодах.
Пропорція антропоморфного квадрата Ga = (√5 + 1). π з'єднує в одну формулу подвійне мажорне золото і срібний перетин. В тРНК живий квадрат припадає на перший елемент стебла молекули. У Періодичний закон та ж пропорція з'єднує кінець VI періоду і перший радіоактивний елемент:
Розберемося щодо початку і кінця VI періоду (елементи 55 і 86):
55 # 8729; Ga = 56,7 → 57 (вихідний елемент першого протуберанця)
86 # 8729; Ga = 88,6 → 89 (вихідний елемент другого протуберанця)
Вихідний елемент другого протуберанця відноситься до початку VI періоду по числу Ф (89 і 55 - два суміжних числа з ряду Фібоначчі), а зв'язок обох вихідних для протуберанців елементів можна виразити так:
Тим же виразом пов'язані пари структурних точок 57/37 і, крім того, - 11/18 і 28/18; 29/19 і 29/46, а також 72/46; 86/55 і 55/87; 111/71.
- Ряд Фібоначчі є лише фрагментом математичної моделі генезису сучасної Всесвіту.
- Найбільша методологічна помилка, котра визначила хід і історії науки, і самої історії людства, зроблена Шеллінгом і Гегелем. Модель тріади була виведена зі сфери діалектики і зведена до «дитячої», схоластичної імітації вже на рівні ланцюга еволюційних тріад.
- Існує елементарна формула еволюційного процесу, що зв'язує корінь з двійки і золотий перетин.
- Гармонія можлива тільки як стійкий стан порушеної симетрії і синтез разнопріродного, тобто як вихід в наступне вимір. Тому вона завжди парадоксальна.
- Точки синтезу в природних гармонійних системах обумовлені пропорцією, еволюційно заданої разнопріроднимі гармонійними константами - золотим перетином, коренем з двійки і числом π.
- Математики, будуючи моделі N мірного простору, працюють в зоні чистої абстракції. Простір - властивість тривимірності. Четвертий вимір нашого світу - його матеріальність.
- Пушкінське твердження «геній - один парадоксів» в першу чергу справедливо по відношенню до самої природи: структури базової тРНК і Періодичного закону елементів засновані на принципі взаємодії ірраціональних і трансцендентних гармонійних констант. Однак якщо в тРНК активно працюють золотий перетин і √2, а число π десь в тіні, то структуру Періодичного закону визначають пропорції золотого і срібного перетину, а √2, хоча і відіграє важливу роль, в графічній моделі структурними точками перегину майже не проявлений. Пояснення в самій графіку моделей: тРНК хрестоподібні (в основі її два пересічних квадрата, але діагональ квадрата і є √2), а в основі структури Періодичного закону, вважаю, лежить коло, тобто саме число π.
М ножество прикладів золотого перетину, відкритих з часів Йоганна Кеплера в самих різних еволюційних об'єктах і явищах, а також повсюдне присутність «дивного числа π» (Раушенбах) в самих різних фізичних і математичних моделях говорять про те, що розгадка механізму гармонійних пропорцій повинна бути знайдена .