Аналогічно виглядають команди чергування і симетрування:
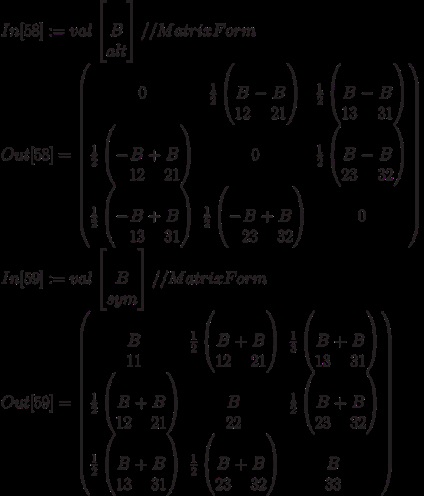
Також часто зручно вивести конкретну компоненту тензора. Це робиться за допомогою явної вказівки списків відповідних індексів:
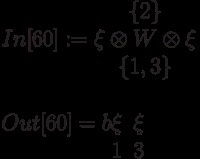
Аналогічно, є можливість породити відразу симетричний або кососімметрічний тензор типу (0, q). Для цього використовуються команди makeSymm, makeSkew, makeSymmTab, makeSkewTab. Для симетричних і до сосімметрічних тензорів визначені операції симетричного твори (SmallCircle, Esc sc Esc) і, відповідно, кососімметрічного твори (Wedge, Esc ^ Esc). Пакет відносить до симетричним (кососімметрічним) тензор або тензори, створені перерахованими чотирма операціями, або отримані в результаті симетрування або чергування тензорів типу (0, q):
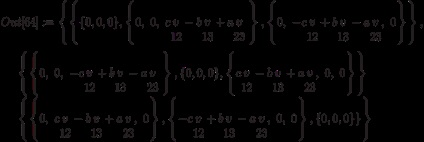
Відзначимо, що при створенні (косо) симетричного тензора по таблиці значень відповідна функція не перевіряє (косо) симетричність таблиці, а просто використовує тільки частину даних, довизначити значення по симетрії:
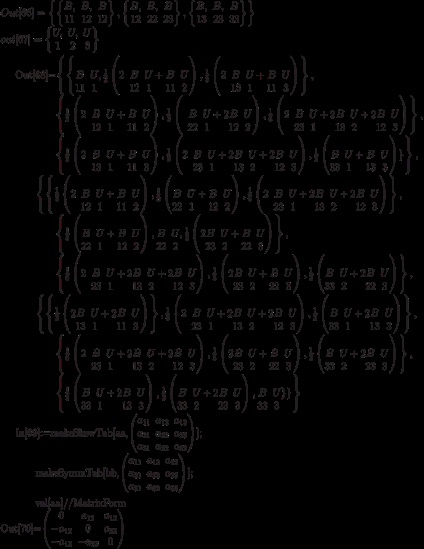
Запис тензора в тензорному базисі, обчислення значення тензора на наборі ковекторов і векторов0. Є можливість записати створений тензор в базисі простору тензорів даного типу:

Для (косо) симетричних тензорів можна скористатися базисом в просторі (косо) симетричних тензорів:
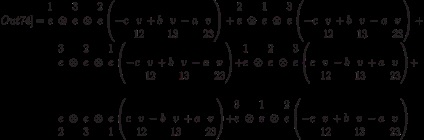
Передбачено також набір зворотних операцій, що обчислюють список компонент тензора, заданого у вигляді лінійної комбінації базисних. Це функції toList, toListSkew, toListSymm:
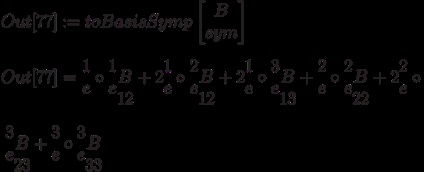

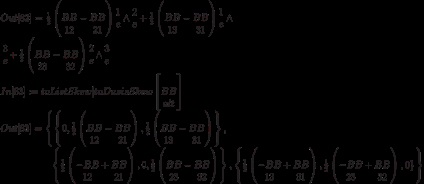
Нагадаємо, що тензор типу (p, q) можна уявляти собі як полілінейное відображення, задане на прямому творі p примірників двоїстого простору і q примірників самого простору. Щоб обчислити значення такого відображення, в пакеті є функція apply:
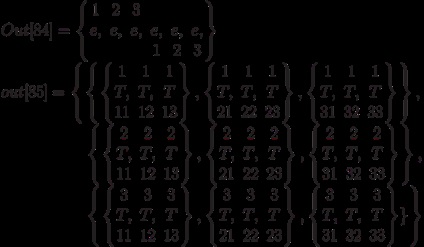
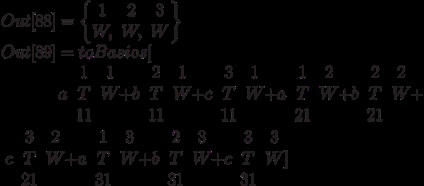
При цьому, як видно з прикладу, є можливість підставляти відразу компоненти тензора. Якщо кількість або вид аргументів не відповідає типу, видається повідомлення про помилку або функція просто не виконується:
Перезапуск. Щоб скасувати всі створені базиси, координати тощо. Слід виконати команду resetTensors:
Особливості роботи з локальними координатами і тензорними полями. Якщо ви задали локальні координати і відповідний базис (команда makeBasisDif), то з'являється можливість задавати тензорні поля, компоненти яких суть абстрактні функції від координат. Відповідний набір функцій - це makeTensorField, makeSkewField і makeSymmField. Результат їхньої роботи - відповідне тензорне поле, до якого можна застосовувати звичайні тензорні операції:
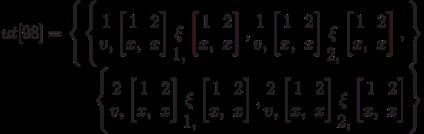
Заміна координат або базису, перерахунок компонент, граф замін. Якщо ми хочемо зробити заміну координат, то слід створити нові координати або новий базис за допомогою команд makeBasisDif і makeBasis. вказавши явно зв'язок нового базису (координат) з яким-небудь вже заданим (за замовчуванням - з поточним) базисом (координатами). У лінійно-алгебраїчних випадку це робиться за допомогою завдання матриці переходу (стовпці якої - суть компоненти векторів нового базису в старому), а в разі локальних координат слід задавати функції переходу, що виражають поточні координати через нові (см. Приклади нижче). Крім того, в якості четвертого аргументу функції makeBasisDif можна налаштувати установки, які визначають зворотне відображення і виражають нові координати через поточні. Перевірка взаємної зворотності залишається на совісті користувача. Якщо перехід заданий, то нові координати стають поточними і значення всіх тензорів автоматично в них перераховують.
Наведемо відповідні приклади. Щоб зручніше було контролювати обчислення, пакет створює орієнтований граф graphBas замін координат (базисів). Вершини цього графа - системи координат. Дві вершини з'єднані стрілкою, якщо відповідна заміна координат задана явно. Цей граф зручно вивести динамічно. У наведеній нижче програмі передбачений перехід до координат, обраним мишкою. А саме, щоб зробити заміну, потрібно клікнути в відповідну вершину графа: