Анотація: Перш ніж починати знайомство з теорією економічних механізмів, доведеться присвятити деякий час теорії, яка абсолютно необхідна для розуміння всього, що відбувається в дизайні механізмів. Мова в цій вступній лекції піде про теорію ігор.
Основні концепції
Дамо формальне визначення ігор, які ми будемо розглядати. До речі, шахи або навіть го не підпадатимуть під це визначення. Що й логічно: ми тут математикою займаємося, а не ефективними алгоритмами; а з математичної точки зору (та й з точки зору теорії складності алгоритмів, асимптотической за своєю природою) шахи або го абсолютно нецікаві: на кінцевій дошці з кінцевої тривалістю партії і з повною інформацією виграшну (або безпрограшну, якщо виграшною немає) стратегію можна "легко "підрахувати простим перебором варіантів.
Ігри, які будемо розглядати ми, теж зазвичай мають на увазі кінцеве (або в теорії безперервне, але в реальності все одно кінцеве, як безліч можливих цін, які гравець може оголосити на аукціоні) безліч можливих стратегій. Але при цьому інформація принципово буде неповною; про це і вся теорія. У нашому розумінні стратегічної гри всі гравці будуть діяти одночасно, і виграш кожного буде залежати від того, які стратегії оберуть всі інші.
Визначення 1.1 .Стратегіческая гра - це трійка
де позначення розшифровуються таким чином:
- - кінцеве безліч гравців.
- - безліч доступних гравцям дій, де - безліч дій, доступних гравцеві. Будемо позначати через дію гравця, а через - вектор дій всіх гравців, окрім i 1 Взагалі, позначення виду в цій книзі зустрічатися будуть повсюдно - звикайте. Через будемо позначати множину всіх векторів дій гравців, через - безліч векторів дій всіх гравців, окрім. Вектор будемо називати профілем дій. або результатом.
- - безліч функцій виплат.
Нас будуть більше цікавити не дії, а стратегії. Стратегія - це те, як агент вибирає свою дію. У засадах теорії ігор це одне і те ж, але в теорії економічних механізмів ми будемо розглядати стратегії, що представляють собою ймовірні розподілу на діях або функції, які беруть до уваги ще й будь-яку додаткову інформацію.
Є і ще одне важливе зауваження: протягом цієї лекції ми припускаємо, що у учасників є переваги з приводу результатів гри і ці переваги можна виразити за допомогою функцій. Це далеко не завжди так, і в "Теореми Ерроу та Гіббард-Саттертуейт" ми ще поговоримо про цікаві ефекти, що виникають, коли переваги так висловити не можна. Але для базової теорії ігор доведеться це припущення все-таки зробити.
Якщо безліч стратегій звичайно, то безліч випадків гри можна висловити -мірною матрицею, в осередку якої з координатами стоять результати. У разі гри з двома гравцями ця конструкція перетворюється в саму звичайну матрицю.
Кінець прикладу 1.1.
Приклад 1.2. Як другий приклад розглянемо класичну гру полковника Блотто [70, 79]. Полковник Блотто повинен розподілити свої сили (солдат) між декількома ділянками поля бою (ділянок). Його противник повинен зробити те ж саме (кількість його солдатів може відрізнятися). Виграє той, хто переможе на більшій кількості ділянок бою.
Наприклад, нехай ділянок бою в грі три, причому і Блотто, і його противник має три солдатами. Тоді безліч стратегій у обох учасників битви складається з наступних елементів:
В результаті у цієї гри виходить ось яка матриця. Тут стратегії Блотто зображені зліва, супротивника - зверху; означає, що переміг Блотто, - що противник, - трапилася нічия.

Кінець прикладу 1.2.
Відзначимо, що в іграх з прикладів 1.1 і 1.2 прибуток одного учасника суворо дорівнювала збитку другого. Такі ігри називаються іграми з нульовою сумою; формально кажучи, в таких іграх для будь-якого профілю дій учасників вірно, що.
Надалі нас будуть цікавити не тільки гри з кінцевими множинами стратегій, але і гри з безперервними такими множинами. Візьмемо класичний приклад - конкуренцію за Курно (Cournot competition) 3 Цей приклад дійсно сходить до класика економічної теорії Антуану Огюстену Курно [14].
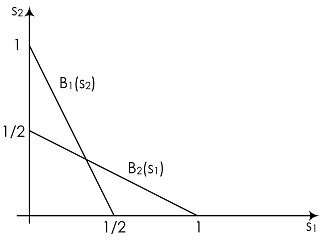
Мал. 1.1. Конкуренція по Курно: функції оптимальної відповіді
Приклад 1.3. Розглянемо ринок якогось продукту, на якому знаходяться рівно дві фірми:. Стратегія кожного з учасників - кількість продукту, яке він справляє:.
Прибуток кожного учасника в результаті гри - це його загальний дохід за вирахуванням собівартості:
де - функція. по якій визначається ціна, а - ціна за одиницю для компанії. Ми будемо припускати, що. В якості опції ми розглянемо
Давайте спробуємо проаналізувати, як фірмам найкраще грати в свою гру. Спробуємо побудувати оптимальну стратегію для гравця, якщо гравець зробив товару (best response function.). Якщо, то виробляти нічого не треба, тому що рівноважна ціна все одно буде дорівнює нулю. Якщо ж, то оптимальну стратегію доведеться шукати так:
Див. Мал. Мал. 1.1. на якому ми зобразили ці функції. Інтуїтивно хочеться сказати, що рівновага буде досягнуто в точці їх перетину; але формально ми про це поговоримо нижче.
Кінець прикладу 1.3.