Бібліографічний опис:
Первинні і вторинні параметри передачі і параметри взаємних впливів кабелів зв'язку визначаються геометричними і електричними параметрами спрямовуючого середовища. Чи не мають загального рішення є завдання оцінювання робочої ємності кабелю і еквівалентної діелектричної проникності середовища між двома провідниками. Рішення даного завдання є актуальним при алгоритмізації автоматичного управління параметрами екструдіруемой пористої ізоляції з введенням межконтурная зв'язку, що забезпечує компенсацію впливу динамічної помилки регулювання одного з параметрів (діаметра або діелектричної проникності ізоляції) на узагальнений параметр якості кабелю (робочу ємність або хвильовий опір) шляхом формування обуреного процесу в контурі автоматичної стабілізації другого параметра (діелектричної проникності або діаме тра ізоляції) [1].
Розглядається задача визначення електричних параметрів кручений пари, яка становить основу радіочастотних кабелів для передачі даних (LAN-кабель). На рис. 1 показано перетин неекранованої кручений пари, що містить дві жили, діаметри ізоляцій яких різні.
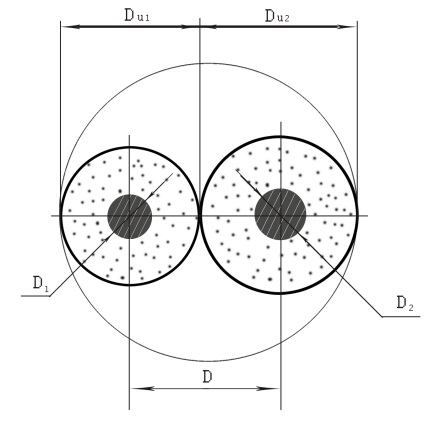
Мал. 1. Перетин LAN-кабель
Традиційно еквівалентна діелектрична проникність спрямовуючого середовища оцінюється як середньозважене значення ізоляції обох жив, з урахуванням співвідношення площ їх перетину. Дана оцінка характеризується невисокою точністю, що неприпустимо при проектуванні і виготовленні кабелів з високою пропускною здатністю. Для оцінки робочої ємності традиційно зупиняються на формулі, виведеної В. Н. Кулешовим [2], яка також характеризується невисокою точністю. Розглядається рішення даної задачі за допомогою конформних перетворень.
Для отримання вихідних співвідношень, що визначають процеси в ланцюгах, використовують первинні параметри ланцюга. Параметри R і L. відображають в еквівалентній схемі (рис. 2) поздовжнє опір ланцюга Z = R + jωL. а параметри C і G - поперечну сумарну провідність ланцюга Y = G + jωC. де R- погонное опір лінії, L - погонна індуктивність, C - погонна ємність лінії, G - погонний коефіцієнт витоку.
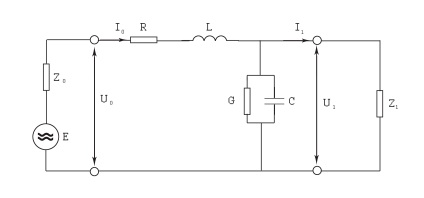
Мал. 2. Еквівалентна схема лінії зв'язку
Якщо значення первинних параметрів ланцюга залишаються незмінними по всій довжині, то такий ланцюг називають регулярної (однорідної) [3]. При цьому активні втрати електромагнітної енергії при її поширення уздовж ланцюга обумовлені первинними параметрами R і G. перший характеризує теплові втрати в провідниках і інших металевих частинах направляючої системи (екран, оболонка, броня), другий - втрати в ізоляції.
Розглянемо однорідну ланцюг з первинними параметрами R, L, C, G (рис. 2). Система диференціальних рівнянь, що визначає напругу і струм в будь-якій точці ланцюга як функції координати x. має вигляд [4]:
Дана система має рацію по відношенню до будь-якої однорідного ланцюга незалежно від її конструкції. Зміна конструкції призводить тільки до зміни значень первинних і вторинних параметрів, в тому числі хвильового опору:
Будемо розглядати LAN-кабель як лінію без втрат. Це означає, що вважаємо витік рівною нулю (G = 0), т. Е. Вважаємо, що простір між провідниками є непровідним. Крім того, нехтуємо втратами в проводах, вважаючи їх ідеально провідними (R = 0). Так як для ідеальних провідників внутрішня індуктивність дорівнює нулю, то в цьому випадку повна погонне індуктивність лінії L зводиться до її зовнішньої індуктивності Le. При цих спрощення формула (2) набуває вигляду:
Для визначення робочої ємності скористаємося конформних перетворенням, використовуючи дрібно-лінійну функцію, яка має вигляд [5]:
де a, b, c, d - постійні, причому ad-bc ≠ 0. Вирішуючи співвідношення (4) щодо z. отримуємо також дрібно-лінійне перетворення:
Дрібно-лінійне перетворення володіє тим властивістю, що будь-яка окружність в площині z переходить в окружність на площині ω і назад, при цьому пряма може розглядатися як коло з нескінченно великим радіусом.
Дрібно-лінійне перетворення володіє також важливою властивістю збереження симетричних точок: воно перетворює будь-яку пару точок z1 і z2. симетричних щодо довільної кола Cz в площині z. в пару точок ω1 і ω2. симетричних щодо Cω - образа окружності Cz на площині ω [5].
Використовуємо властивість дробу лінійного перетворення зберігати окружності, і відобразимо область між жилами LAN-кабель (рис. 3) на концентричне кільце, яке є простою двохзв'язной область.
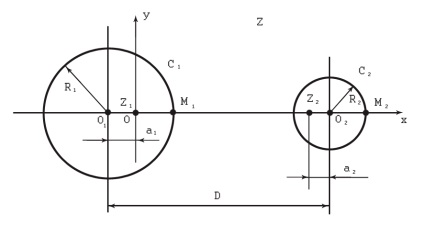
Мал. 3. взаимоположение жив LAN-кабелю в площині Z
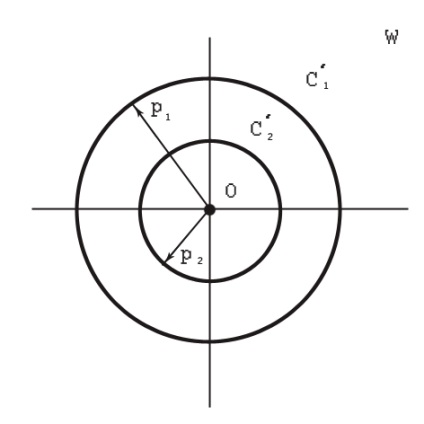
Мал. 4. взаимоположение жив LAN-кабелю в площині W
Якщо розшукати положення точок z1 і z2. одночасно симетричних відносно обох даних кіл С1 і C2. які збігаються з поверхнями електродів, то при відображенні
кіл С1 і C2 перейдуть в окружності С'1 і C'2. для яких точки ω1 = 0 і ω2 = ∞ також будуть симетричними. Звідси випливає, що окружності С'1 і C'2- концентричні, і їх центр збігається з початком координат в площині ω. що дає можливість визначити робочу ємність, яка виникає між жив LAN-кабель, за відомою формулою для сферичного конденсатора (рис. 4).
Знайдемо тепер симетричні точки щодо кіл С1 і C2. З рис. 3 маємо:
де введені позначення
Помістивши початок координат в симетричній точці Z1. розташованої в колі С1. отримаємо:
т. к. легко переконатися, що
отже, функція ω набуде вигляду:
Беручи до уваги властивість збереження незмінної величини ємності при конформних перетвореннях, знайдемо останню в площині ω для паралельно розташованих жил кабелю [5]:
вираз (12) набуде вигляду:
Щоб визначити еквівалентну діелектричну проникність εекв знову скористаємося конформних відображенням, але тепер відобразимо площину z (рис. 5) на площину t (рис. 6),
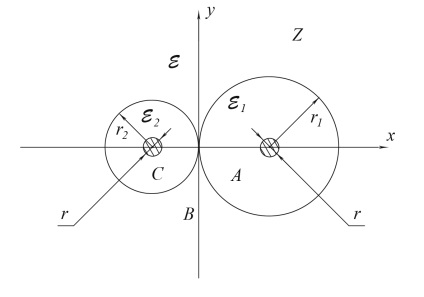
Мал. 5. взаимоположение жив LAN-кабелю з ізоляцією в площині Z
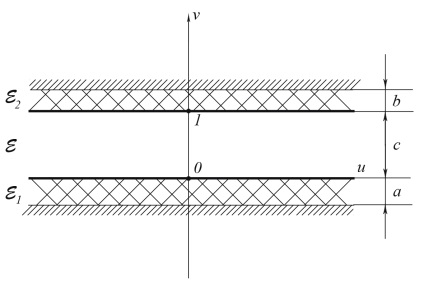
Мал. 6. Результат відображення площині z на площину t
Для даного відображення необхідно щоб виконувалася така умова [5]:
Визначимо u і v. враховуючи вирази (15), (16) і (17):
Відобразивши площину z на площину t. ми отримали плоский конденсатор з нескінченними пластинами. В даному випадку представляється можливим визначення його діелектричної проникності. Вона і буде невідомої еквівалентної діелектричної проникністю середовища між двома провідниками.
Для вирішення даного завдання отриманий конденсатор можна розділити на три последовательносоеденнених конденсатора з однорідними діелектриками між їх пластин з відповідними діелектричними проницаемостями: ε1. ε2. ε (рис. 7).
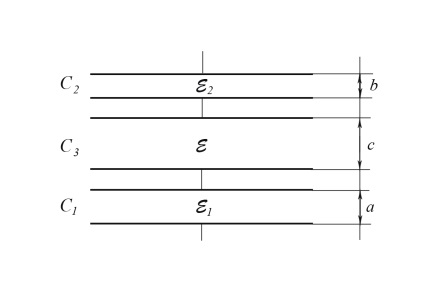
Мал. 7. Еквівалентна схема з'єднання трьох конденсаторів з однорідними діелектриками між їх пластин
Загальна ємність схеми С. розташованої на рис. 7 визначається з виразу:
Підставивши параметри конденсаторів в вираз (19), отримаємо:
З виразу (20) випливає, що:
Ємність конденсатора вираховується за формулою:
де l - відстань між пластинами:
З виразу (21) введемо змінну m:
З огляду на вираження (21) - (24) отримаємо:
Залишається лише знайти відстані a, b, c, визначивши координати точок на площині t (рис. 6), що мають на площині z (рис. 5) координати:
Використовуючи вираз (18), отримаємо координати цих точок на площині t відповідно:
Підставивши вирази (24), (26) - (27) у вираз (25), і враховуючи, що:
де Dі1. Dі1 - діаметри ізоляцій відповідно, d - діаметр провідної жили, отримаємо:
У вираз (14) підставимо (28), і враховуючи, що:
Вираз (29) справедливо і для екранованої кручений пари LAN-кабель, якщо ввести в нього коефіцієнт екранування і коефіцієнт скрутки.
Миролюбов, Н. Н. Методи розрахунку електростатичних полів. - М. Наука, 1963.
Основні терміни (генеруються автоматично). діелектричної проникності, кручений пари, робочої ємності, діелектричної проникності ізоляції, еквівалентної діелектричної проникності, окружності С1, окружності С2, діелектричної проникності середовища, проникності ізоляції кручений, первинними параметрами, радіус кола С2, погонне індуктивність, діаметри ізоляцій, внутрішньому колу С1'определім, параметрів кручений пари, еквівалентної діелектричної проникністю, робочої ємності кабелю, електричними параметрами направляючої, кабелів зв'язку, робочу ємність.