односмуговий гіперболоїд x 2 / a 2 + y 2 / b 2 - z 2 / c 2 = 1 a> 0, b> 0, c> 0; Перетнув. координатні осіплоскостямі x = 0, y = 0, z = 0 по гіпербол y 2 / b 2 - z 2 / c 2 = 1 x 2 / a 2 - z 2 / c 2 = 1 і еліпсоїд x 2 / a 2 + y 2 / b 2 = 1 відповідно. У перетинах однополосного гіперболоїда площинами z = h завжди виходять еліпси x 2 / a 2 + y 2 / b 2 = 1 + h 2 / c 2 з півосями і.
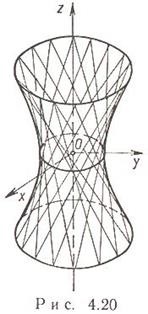
a = b - однопорожнинний гіперболоїд обертання навколо осі Oz.
Перетину однополостного гіперболоїда площинами - або еліпс, або парабола, або гіпербола, або пара прямих (прямолінійних створюючих).
Через довільну точку проходять дві прямолінійні утворюючі з направляючими векторами і де:
Зокрема, якщо точку вибирати на горловому еліпсі то рівняннями прямолінійних утворюють будуть:
Двуполостной гіперболоїд, його канонічне рівняння.
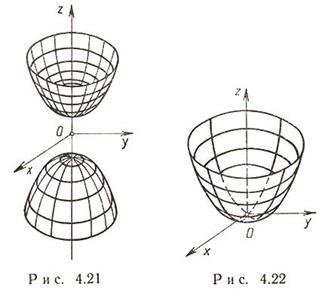
двуполостной гіперболоїд x 2 / a 2 - y 2 / b 2 - z 2 / c 2 = 1 a> 0, b> 0, c> 0; x = h виходить еліпс x 2 / a 2 + z 2 / b 2 = -1 + h 2 / c 2 з півосями b * Корінь (h 2 / a 2 -1) і з * Корінь (h 2 / a 2 - 1). При h = a отримаємо в перетині точки (± а, 0,0) - вершини двуполостного. У перетинах координ пл. z = 0 і y = 0 отримаємо гіперболи x 2 / a 2 - y 2 / b 2 = 1 і x 2 / a 2 - z 2 / c 2 = 1 відповідно.
a = b - двуполостной гіперболоїд обертання навколо осі Oz.
Перетину двуполостного гіперболоїда площинами: або еліпс, або гіпербола, або парабола, або точка, або.
Еліптичний параболоїд, його канонічне рівняння.
еліптичний параболоїд x 2 / a 2 + y 2 / b 2 = 2pz a> 0, b> 0;
p = q - параболоїд обертання навколо осі Oz.
Перетину еліптичного параболоїда площинами - або еліпс, або парабола, або точка, або.
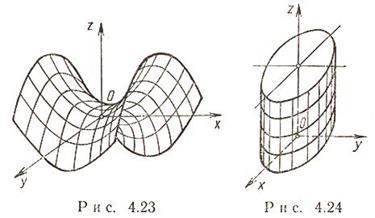
Гіперболічний параболоїд, його канонічне рівняння. Сімейства прямолінійних утворюють гіперболічного параболоїда.
гіперболічний параболоїд x 2 / a 2 - y 2 / b 2 = 2pz a> 0, b> 0;
Перетину гіперболічного параболоїда площинами - або гіпербола, або парабола, або пара прямих (прямолінійних створюючих).
прямолінійні утворюючі
Через кожну точку проходять дві прямолінійні утворюючі:
Поверхнею обертання називається поверхня, утворена обертанням будь-якої плоскої лінії навколо прямої, що лежить в площині цієї лінії.
Для виведення рівняння поверхні обертання необхідно вибрати систему координат. Щоб рівняння поверхні обертання виглядало простіше, вісь обертання приймають за одну з координатних осей.
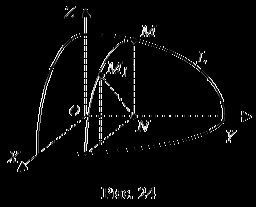
Нехай в координатної площини Oyz задана крива L рівнянням F (Y, Z) = 0 (рис. 24). Обертаємо криву L навколо осі Oy. Отримаємо деяку поверхню. Нехай M (x, y, z) - довільна точка вийшла поверхні. тоді
. але тому що якщо взяти точку M1 з негативною аплікатою, то
Отже, маємо Y = y, і координати точки M (x, y, z) задовольняють рівняння
Рівняння (62) і є шукане рівняння поверхні обертання.
Т. о. щоб отримати рівняння поверхні, утвореної обертанням лінії L, що лежить в площині Oyz, навколо осі Oy, потрібно в рівнянні цієї лінії замінити z на
Аналогічні правила будуть мати місце і по відношенню до рівнянь поверхонь, отриманих обертанням плоских ліній навколо інших координатних осей.
циліндри другого порядку: еліптичний циліндр x 2 / a 2 + y 2 / b 2 = 1 a> 0, b> 0; гіперболічний циліндр x 2 / a 2 - y 2 / b 2 = 1 a> 0, b> 0; параболічний циліндр y 2 = 2px; пара пересічних площин a2x2-b2y2 = 0 a> 0 b> 0 пара паралельних або співпадаючих площин x-a = 0 a> = 0; пряма x 2 + y 2 = 0
конус другого порядку x 2 / a 2 - y 2 / b 2 - z 2 / c 2 = 0 a> 0, b> 0, c> 0; Перетинаючи пл. z = h -> x 2 / a 2 + y 2 / b 2 = 1. У перетині площинами x = 0 y = 0 маємо пари перетнув прямих y 2 / b 2 - z 2 / c 2 = 0; x 2 / a 2 - z 2 / c 2 = 0 соотв.