На рис. 12 показано при-трансформаційних змін двохщілистими антени об-ратного випромінювання, відомого під назвою опромінювача Катлера.
При такому облучателе антенна система виходить компакт-ної в конструктивному відношенні. Опромінювач має менший ті-Невою ефект, ніж інші облучатели.
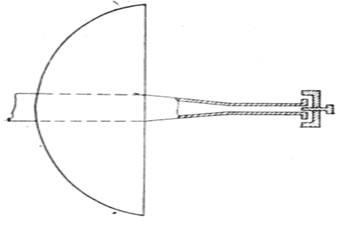
Діаграма спрямованості такого опромінювача залежить від дли-ни і ширини щілин і від відстані щілин від стінки хвилеводу. Отже, вона може бути регульована і підібрана опти-мальної відповідно до вимог. Регулювання осуществля-ється експериментально.
Фазовий фронт хвилі, випромінюваної цим облучателем, являє-ся майже сферичним. Фазові спотворення, що мають місце через відбиття від стінок хвилеводу, не перевищують 30 °.
Широкосмугові облучатели кругової поляризації.
На рис. 13а-г показана група облучателей дзеркал, розрахованих на роботу в широкій смузі частот і створюють поле випромінювання кругової поляризації: відповідно циліндрична спіраль, плоска спіраль, конічна спіраль, логоперіодична антена
Дводзеркальні параболічні антени.
Схема двухзеркальной антени.
У ряді практичних випадків знаходять застосування дводзеркальні антени, зображені схематично на рис. 14 і 15.
Двухзеркальная антена складається з опромінювача 1, освещающе-го поверхню невеликого дзеркала 2, від поверхні якого хвиля прямує на велике дзеркало 3. Після відображення від великого дзеркала в його розкриваючи створюється синфазное поле. Бу-дем надалі користуватися термінами: «мале дзеркало» і «велике» чи «основне дзеркало». Харчування до опромінювача підщепі-диться фідером 4 від передавача (приймача) 5.
Процеси переизлучения малим дзеркалом і формування по-ля в розкриві основного дзеркала прийнято в теорії антен трак-Това з позицій геометричної оптики, користуючись концепцією падаючих і відбитих променів. При досить великому (в оди-Ницаха довжини хвилі) відстані опромінювача від малого дзеркала і останнього від основного рефлектора, а також при досить великому радіусі кривизни обох дзеркал таке трактування дає хороше наближення до істинного. Тому можна стверджувати, що сферична хвиля, излученная з фокуса параболоїда, пре-утворюється дзеркалом в плоску, і виходячи з будь-якого фокусу гіперболоїда або еліпсоїда після переизлучения збереженні-вується сферичну форму фронту хвилі. При цьому її фазовий центр переноситься в другій фокус малого дзеркала. Якщо другий фокус (точку фазового центру) поєднати з фокусом параболоїда, то після другого переизлучения від параболоїда утворюється плоска хвиля. Малюнок 14.16б ілюструє ці положення на прикладі малого дзеркала гіперболічної форми. Мале гіпер-боліческіе дзеркало 2, 2 ', 2 "може бути звернено в бік па-раболіческого опуклістю 2 або увігнутістю 2'. Проміжне становище між опуклим і увігнутим Гіперболоїд зани-томить площину 2 ''. У разі .плоского малого дзеркала 2" пере-излученная сферична хвиля має фазовий центр на расстоя-ванні дзеркального зображення точки фазового центру опромінювача. Мале еліптичне дзеркало 2 ' "показано на рис. 14 а. Воно звернене завжди увігнутістю до параболічного.
Наведені на рис. 14 б і 15 схеми двохдзеркальних ан-Тенн з малими опуклими і увігнутими дзеркалами запозичені з астрономічної оптики і названі відповідно іменами винахідників дзеркальних телескопів Кассегрена і Грегорі (антена Кассегрена - рис. 14 а, антена Грегорі - рис. 15 а).
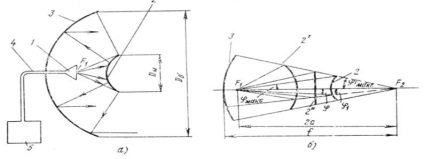
На рис. 15 б показана так звана антена зі зміщений-ної віссю. Більш докладно вона описується нижче.
Можливі дводзеркальні антени з синтезованими по-поверхні великого і малого дзеркал, підібраними з усло-вия оптимальності характеристики.
Двухзеркальная антена Кассегрена.
Нагадаємо, що у антени Кассегрена велике дзеркало 3 параболічної форми, а мале (префокальное) 2 - гіперболічний-ської. Воно поміщено, як показано на рис. 16, опуклою сто-роною до великого дзеркала. Фазовий центр опромінювача 1 распо-покладається в фокусі fi гіперболічного відбивача; другий фо-кус F2 гиперболоида поєднується з фокусом параболічного зер-калу. Сферична хвиля опромінювача трансформується малим дзеркалом в сферичну ж хвилю, але з центром в F2. яка, в свою чергу, трансформується великим дзеркалом в плоску хвилю, яка створює в розкриві синфазное поле.
При розрахунку двохдзеркальних антен зручно користуватися по-заняттям еквівалентної 4 однозеркальная параболічної антени, графічне побудова профілю якій для антени Кассегрена ілюструється рис. 16. Через крайні точки кривої а й b великого дзеркала проводяться прямі, паралельні осі антени; з фокуса fi проводяться дві прямі через краю малого зер-кала до перетину в точках а 'і Ь' з прямими аа 'і bb'.
Через точки а 'і Ь' проводиться парабола з фокусом в точці F1. На рис. 16 показано графічне побудова цієї параболи 4.
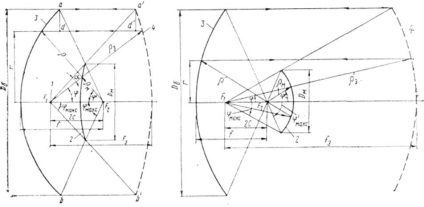
З точок f1 і F2 проводяться через одну і ту ж точку малого зер-кала радіуса-вектори, ρ і ρ0. З точки перетину р з великим дзеркалом проводиться паралельна пряма до прямої аа 'до перетину з ρ е. Такі точки перетину і утворюють еквівалентну дзеркало 4. Легко бачити, що основне дзеркало антени і еквівалентні-валентна парабола взаємні по відношенню до гіперболи малого дзеркала. Якщо побудувати двухзеркальной антену, беручи в якості великого дзеркала еквівалентну параболу, як малого дзеркала - той же гіперболоїд, але звернений увігнутою сторо-ною до великого дзеркала, і помістити опромінювач в точці F2. тоді основне дзеркало антени буде еквівалентною параболою.
Будь-які два променя, які виходять один з точки F1 в сторону еквівалентні-валентної параболи, інший - з точки F2 в сторону параболи антени і проходять через одну і ту ж точку малого дзеркала, відбиваються від відповідних великих дзеркал по одній пря-мій назустріч один одному. Розглядаючи вузький пучок променів з кутовим розміром а, можна помітити, що у розкриття двухзер-кальной антени і еквівалентної однозеркальная площа перетину пучків буде однаковою (ad - a'd ') і оскільки енергія, пе-реносімая через ці перетину, одна і та ж, то і щільності енер-гии, а отже, амплітудні розподіли поля в обох апертурах виявляться тотожними. Це дозволяє при визна-лення поля випромінювання двухзеркальной антени Кассегрена вирішувати це завдання для еквівалентної однозеркальная антени.