Визначення природного тригранника Френе. Проекції швидкості і прискорення точки на його осі. Приклад визначення ортов природного тригранника.
На сторінці "Кінематика матеріальної точки" ми встановили, що вектор швидкості руху точки спрямований по дотичній до траєкторії. Вектор прискорення лежить в дотичній площині і його можна розкласти на дві складові. Одна складова спрямована по дотичній до траєкторії. Друга складова спрямована перпендикулярно дотичній, в сторону миттєвого центру кривизни траєкторії.
У деяких випадках зручно ввести систему координат, пов'язану з поточним становищем точки. Розглянемо точку в певний момент часу. Вважаємо, що нам відома траєкторія її руху. Проведемо через точку три прямих - дотичну до траєкторії, головну нормаль і бінормаль. Головна нормаль перпендикулярна дотичній і спрямована в бік миттєвого центру кривизни траєкторії. Бінормаль перпендикулярна дотичній і головною нормалі. Виберемо систему координат з початком в точці і осями, направленими уздовж цих прямих. Таку систему координат називають природним тригранник Френе. Осі цієї системи координат називаються осями природного тригранника.
Орти природного тригранника
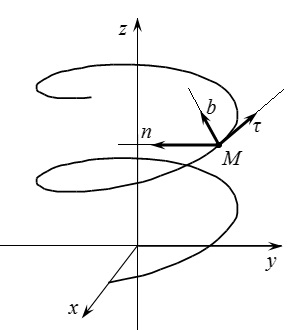
Нехай. і - одиничні вектори, спрямовані уздовж дотичній, головною нормалі і бинормали до траєкторії, відповідно. Ці вектори є ортами обраної нами системи координат або ортами природного тригранника. Розглянемо питання про вибір напрямку цих векторів.
Вектор спрямований уздовж дотичній до траєкторії. Тому можна вибрати два взаємно протилежні напрямки. Найзручніший спосіб - це направити уздовж вектора швидкості точки. тоді
.
Однак, це не завжди можна зробити. Зустрічаються випадки, коли траєкторія руху заздалегідь відома, а швидкість - немає. Наприклад, при русі точки по жолобу всередині твердого тіла під дією зовнішніх сил. У таких випадках напрямок вектора вибирають заздалегідь. Наприклад, в сторону зростання дугового координати.
Напрямок одиничного вектора головною нормалі визначено однозначно. Він спрямований перпендикулярно. в сторону миттєвого центру кривизни траєкторії.
Вектор бинормали спрямований перпендикулярно векторах і так, щоб три вектора. і утворили правостороннім систему координат:
.
Швидкість і прискорення точки в тригранник Френе
Вважаємо, що вектор збігається за напрямком з вектором швидкості точки. Тоді можна застосувати формули, які ми вивели на сторінці "Кінематика матеріальної точки".
Тобто, в природному тригранник з ортами. швидкість має одну компоненту:
.
рівну модулю швидкості. Іншими словами, модуль швидкості - це проекція вектора швидкості на вісь природного тригранника. Проекції вектора швидкості на осі і тригранника дорівнюють нулю.
Прискорення має дві компоненти:
.
Цими компонентами є дотичне і нормальне прискорення:
;
.
Тобто дотичне і нормальне прискорення - це проекції вектора прискорення на осі і природного тригранника. Проекція вектора прискорення на вісь дорівнює нулю.
Як визначити осі природного тригранника
Далі ми вважаємо, що у нас є нерухома система координат. Матеріальна точка здійснює рух. Потрібно знайти осі природного тригранника. Тобто визначити проекції ортов. і в системі координат.
Для координатного і векторного способів завдання руху
Для координатного і векторного способів завдання руху точки, формули для визначення ортов представлені на сторінці "Кінематика матеріальної точки". На сторінці "Координатний спосіб завдання руху точки" розібраний приклад обчислення компонентів векторів.
Тобто, щоб визначити орт природного тригранника, потрібно знайти компоненти векторів швидкості і нормального прискорення. застосовуючи такі формули:
;
;
;
.
Далі визначаємо орт природного тригранника:
;
;
.
Для природного способу завдання руху
За природного способу завдання руху точки нам відома траєкторія її руху. Тому перед нами стоїть завдання - за відомою траєкторії, визначити орт природного тригранника. Якщо траєкторія являє собою просту геометричну фігуру, наприклад коло, то визначити вектори. і можна геометрично.
Загалом, і більш складному випадку, потрібно представити рівняння траєкторії в параметричному вигляді. Для цього вводимо параметр. Це можна зробити багатьма способами. Тому бажано вибрати найбільш зручне представлення.
Нехай, наприклад, траєкторією руху є еліпс, що лежить в площині.
.
Найбільш зручний параметричне представлення можна отримати, якщо скористатися тригонометричної формулою:
.
Тоді рівняння траєкторії має вигляд:
Тут - параметр.
Це не єдиний спосіб отримати параметричне представлення. Можна, наприклад, дозволити рівняння еліпса відносно.
.
Застосовуючи цю формулу, отримаємо інше параметричне представлення:
Далі вважаємо, що ці параметричні рівняння описують рух матеріальної точки, в якому параметр грає роль часу. Тоді, для визначення осей тригранника, можна застосувати формули, що застосовуються для векторного і координатного способів завдання руху. Обчислені, таким чином, швидкість і прискорення будуть залежати від обраного параметричного уявлення. Але геометричні характеристики траєкторії, такі як орти. і радіус кривизни траєкторії не залежить від обраного параметричного уявлення.
Отже, щоб знайти орт природного тригранника по заданій траєкторії руху. потрібно представити рівняння траєкторії в параметричному вигляді і застосувати формули, що застосовуються при координатному способі завдання руху.
Приклад визначення ортов природного тригранника
Знайти одиничні вектори в напрямку осей природного тригранника, а також радіус кривизни траєкторії, для циліндричної гвинтової лінії з радіусом підстави і кроком.
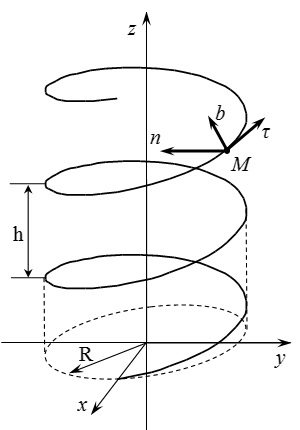
Виберемо систему координат. Ось направимо уздовж осі гвинтової лінії. Тоді рівняння лінії можна представити в наступному параметричному вигляді:
(1)
Тут - параметр ;. Якщо взяти проекцію точки лінії, на площину. то - це кут між віссю і проекцією. При збільшенні на. координати і точки повертаються в первісної положення, а координата збільшується на.
Вважаємо, що рівняння (1) описують рух точки по гвинтовий лінії. Визначаємо кінематичні величини для такого руху.
Диференціюючи рівняння (1) з. знаходимо компоненти вектора швидкості:
;
;
.
Квадрат швидкості:
.
Модуль швидкості:
.
Одиничний вектор в напрямку дотичної до траєкторії:
.
Диференціюючи компоненти вектора швидкості по. знаходимо компоненти вектора прискорення:
;
;
.
Дотичне прискорення - це проекція прискорення на напрямок вектора.
Цей результат можна отримати і більш простим способом. Для цього врахуємо, що модуль швидкості не залежить від і застосуємо формулу:
.
Вектор дотичного прискорення:
.
Вектор нормального прискорення:
Квадрат вектора нормального прискорення:
.
Модуль вектора нормального прискорення:
.
Радіус кривизни траєкторії:
.
Одиничний вектор в напрямку головної нормалі траєкторії:
.
Одиничний вектор в напрямку бинормали: